马尔科夫链(Markov)

简要介绍马尔科夫链

来源：以下内容节选自知乎

作者：许铁-巡洋舰科技

链接：https://www.zhihu.com/question/26694486/answer/349872296

经典表述

$$Pr(X_{n+1}=x|X_1=x_1,X_2=x_2,…,X_n=x_n)=Pr(X_{n+1}=x|X_n=x_n)$$

马尔科夫链的核心条件概率表达式就是这台火车链接不同车厢的链条。 如果这个条件概率关系不随时间变化，我们就得到经典的稳态马尔科夫链。它有一个良好的性质，就是当这个过程启动一段时间就会进入统计稳态，稳态的分布函数与历史路径无关。

一个简单的例子

关于生育偏好是否影响男女比例的问题。

我们知道过去的人喜欢生男孩，往往生女孩子就不停生，直到生到一个男生为止，因此就造成很多一大堆姐姐只有一个弟弟的家庭。我接触过的一些特别聪明的人都会认为这样的行为会影响男女比例。大部分人觉得会造成女孩比例多，少数人认为会增加男孩比例。 实际呢？

一言以蔽之： 不变。 为什么？ 生育问题是典型的稳态马尔科夫过程，下一次生育不受上一次生育的影响。 根据马氏过程的特性，你知道历史无需考虑历史路径， 最终的平衡概率只取决于每一步的概率。所以无论你怎么玩，不论是你拼命想生男孩还是女孩，都无法影响人口比例。

但是有一招却是有影响的，就是打胎。 为什么？ 答案依然很简单，你改变了每一步的概率。

这就是马尔科夫过程的威力和魅力，可惜人生却不是马尔科夫过程， 因为每一步都高度依赖于过去n步，因此人生是高度历史路径依赖的。

稳态Markov过程

如果说markov过程每一步与前一步的关系是与时间无关的，即当前其中的概率关系是不变的，则这个过程就是稳态的。

$$Pr(X_{n+1}=x|X_n=y)=Pr(X_{n}=x|X_n-1=y)$$

在这个极度简化的模型下，markov process 可归结为一个在态空间里的跃迁轨迹。下图的随机变量是横轴（a，b，c，d四个态），时间是纵轴。系统从此刻的态跃迁到下一刻的态都是随机的，而且跃迁的概率由一个数字决定，这个数字不由轨迹的历史决定，因而markov。从此刻任一状态到达下一刻任意状态包含4x4个概率，因此可以写作一个4x4的跃迁矩阵。跃迁矩阵Pij涵盖了过程的全部信息。

信息

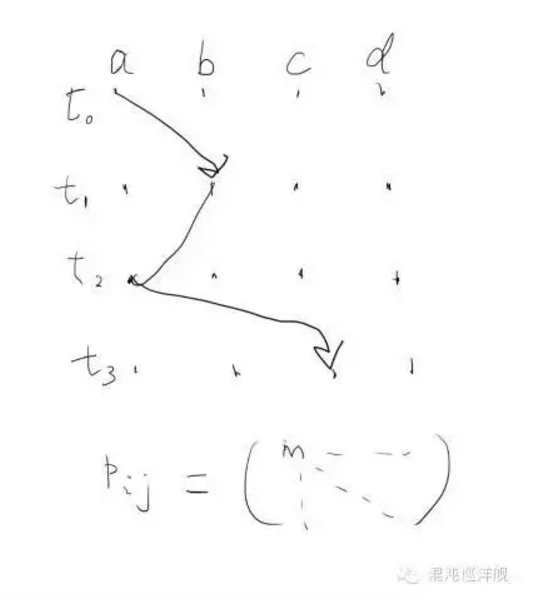
相当于穷举出了所以可能的转移概率，下面还有张更通俗的图

稳态过程的特征量

稳态过程含有两个个重要的特征量： 平均值和自相关函数（Auto-correlation），稳态（stationary）的含义正是在平均值附近扰动，在这个情况下随机性换以另外一个名词-fluctuation（扰动）。 而在非稳态下，扰动和平均值的概念变得模糊，失去意义。

平均值自然重要，但扰动却往往包含着平均值所没有的信息。 首先我们计算方差，来看扰动的剧烈程度，但是这远远不够。

Auro-correlation和之前描述的相关性具有内在的联系，事实上它描述的就是此时的扰动和彼时的扰动的相关性。

$$R(\tau)=\frac{E[(X_t-\mu)(X_{t+\tau}-\mu)]}{\sigma^2}$$

这个量可以理解为你手里有一个信号，首先你减去平均值，这样信号就在0附近扰动。 你把这个信号平行移动一个时间差， 然后把它和原来的信号乘起来，如果说信号本身代表的过程在时间上胡乱跳跃无迹可寻， 那么这个量就很接近0，因为正和负的部分无序的乘起来，正负互相抵消，你的期望就是0。反之，如果你的信号内包含内在的构造（pattern），就会得到不为0的值。

备注

这个感觉有点像正交性

因此，日常生活中你手里具有的往往是数据，你什么都不知道的时候，计算这个量就是起点，这个东西在帮你寻找无序中的结构（pattern），它将告诉我们系统噪音的性质。

比如我们经常说的白色噪声（white noise）的定义就是自关联性为0， 因为它要的是绝对的无序， 毫无记忆，毫无结构。这种信号就是最基本的噪声形态。

而如果我们发现一个随时间差变化很慢的自相关函数，往往显示系统具有记忆的特性，因而产生了更复杂的结构， 或者系统临近相变。

自相关性的计算告诉我们的是， 你不要只看表面的无序有序，因为人眼喜欢在无序中寻找有序，而一个有力的计算就可以告诉你比你的眼睛更准确的信息。

master equation

刚才描述离散的markov过程，如果一个过程是连续的，不再分为第一步第二步第三步， 我们就可以用微分方程描述一个马尔科夫过程。 这就是master equation - 所谓大师方程。 这是物理，化学，经济学，得到一些给力结果经常用到的微分方程。

master equation直接关注的是随机过程的全貌。刚才所说的跃迁轨迹是一次实验的结果，而Master Equation 描述的却是无数实验者同时入场，进行马尔科夫过程，你会看到一个新的图像。系统每一个时刻的状态不再是态空间一个具体的点，而是一大团点（一大丛实验者），它们慢慢的在态空间里运动，我们可以统计站在不同的状态上的实验者个数，因而得到的是一个概率分布，正是之前说的分布函数的概念。 物理经常用概率云，概率波一类的词描述这种情境。 其实都是在说我们不再用一个数字描述世界，比如速度，位置，而是这个值的分布函数。变化的不再是某个特定的值而是它的分布函数。

状态空间的分布函数，又可称作场。由此，场的物理学可以徐徐入场。

之前说的马尔科夫过程的关键-联系此刻与下一刻的条件概率，在这里以跃迁矩阵A表示。

刚才讲到牛顿力学和马尔科夫过程有着内在的联系，Master equation就是随机过程里的牛顿第二定律。这个方程对于解释很多物理化学里的随机过程有神一般的效力。他就是概率场的动力学方程。

$$\frac{d\vec{P}}{dt}=A(t)\vec{P}$$

A就是跃迁矩阵，而向量P即概率场，就是经过时间t，系统状态的分布函数。该方程指示了概率会如何随时间变化。

由此我们看到用Master方程研究问题的好处，转不确定为确定。当你站在纵览所有可能性的制高点，把所有可能性看做高维空间的“概率场”。 不确定性的随机游走变成了概率分布函数（概率场）的确定性演化。这也是为什么场物理在近代物理后成为主导，所研究对象多为随机过程。

量子力学大名鼎鼎的薛定谔方程，其实说的也是这回事，我们无法同时确定电子的位置和动量，因为我们转而求其概率分布函数， 得到一个类似Master equation的微分方程，只不过数学形式更复杂，但思维都是转而研究概率的动力学。 这个方程却干掉了一个物理史上的超级难题， 如果在考虑微观世界的不可确定下预测它们的运动。

注意

稳态解：master equation 指导系统演化，如果A（t）不含时间， 就得到刚才说的稳态过程，系统会演化成一个稳定状态，即分布函数不再随时间变化。A*P=0 我们通常称为平衡态

一些经典的Markov例子

分叉过程 Branching Process

分叉过程 ，一个祖先繁衍的后代， 会出现多少个家庭， 每个家庭人口是怎么分布的？

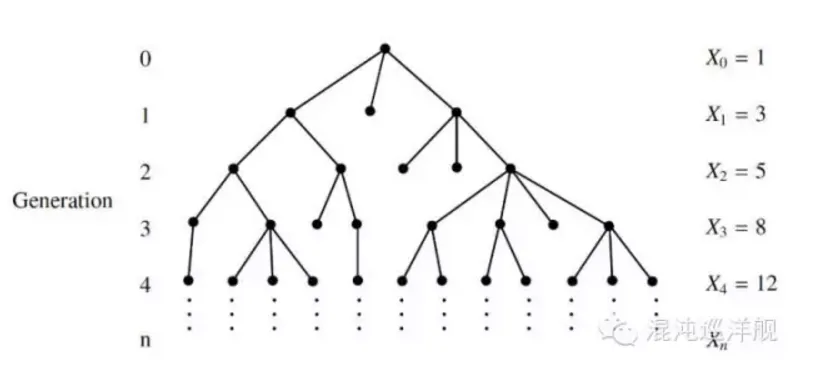
所有家族的演化，生物种群的繁殖，都可以用这个模型研究。一个个体可以繁殖出的子嗣数量是一个随机变量，经过n代之后将形成一个由大小迥异的家族组成的群体。

如果对应为一个随机过程：-每一代的人口数就是就是随机变量，我们要研究的就是与这个随机变量对应的分布函数。

这个过程具有的典型性质是迭代： 如果上一代的人口数Gn，下一代就是Gn+1=G（Gn），给定第n代的家族人口分布，那么下一代的家族人口分布只与上代有关。所以这个是典型的Markov process

这个问题可以推出一些有趣的问题， 比如人口中各大姓氏的比例。 一般情况下，各大姓氏的比例在各个种群中符合相同的统计规律（幂律），就是Branching Process 的结果。

泊松过程 Poission Process

比如一个小旅店里一晚上到来的客人数量随时间的变化，或者光子枪喷出的光子数, 一个帖子两分钟内的访问次数，都是再经典不过的例子了。

泊松分布由二项分布演化而来。二项分布十分好理解，给你n次机会抛硬币，硬币正面向上概率为p，那么n此抛出有k次朝上的概率有多少？ 这是一个经典的二项分布。当这里的概率p趋于0，而n趋于无穷，我们就得到一个泊松分布。泊松分布多用于连续时间上的问题， 如果概率在连续的时间上是均匀不变的（任意时候发生的概率为P），我们就有一个泊松过程。这也极好理解，只要你把时间切割成小段。 比如打开一个帖子的两分钟访问者的概率分布问题，你把两分钟分成120秒， 每秒上有访问者进入的概率是确定的，那么这无非就是投120次硬币多少次向上的问题， 由于微小时间尺度上一件事情发生的概率通常很小，因此，泊松分布通常成立。

$$P(X=x)=\frac{\lambda^x-e^{-\lambda}}{x!}$$

泊松分布一般的形状，三条曲线代表了平均值不同的三个泊松分布：

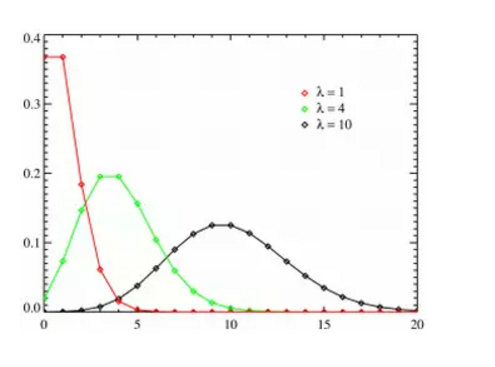
泊松过程，恐怕是最简单的随机过程，也是所有随机过程的参考系-好比物理的惯性定律。我们研究一个随机过程时候，第一个做的就是与泊松做比较。

为什么泊松是一切随机过程的参考系？因为泊松是一个此时的变化和彼时毫无联系的过程，或者说此刻和下一刻是完全独立的，markov说的是与此时只允许与上一个时刻有联系，而泊松就更近一步，把这种联系也取消掉。

如果我们假定每件事件的发生都与其它时刻事件的发生无关，我们就可以试图用泊松分布表述它。比如一个商店前台顾客的光临，一般情况下，每一个顾客的到来都与前一个顾客无关，因此一段时间内前台顾客的数量符合泊松分布。

反过来，判断一个随机过程的前后事件是否独立，也可以通过它是否符合泊松分布判别，如果你得到的统计分析偏离了泊松，通过是前后事件相关联的标志。 事实上生活中的事情都偏离泊松，而是具有强大的关联性。 比如你一周内收到的邮件，通过在周一早上爆发而来，而在周末减少到零。你在一段时间会不停叫桃花运，而后一段十分冷清等。 这些都告诉你要找找背后的原因。

维纳过程 Wiener Process

Wiener Process， 其原型就是大名鼎鼎的布朗运动。这恐怕是在自然科学以及经济金融里用的最广泛的随机过程。也是随机过程的灵魂基础。

关于Wiener Process， 最有趣的比喻是随机游走的醉汉。醉汉在一条直线上移动，往左或往右的概率相等。醉汉走出去的距离与时间的关系，就是Winner Process。

上上下下的随机游走表现的美丽轨迹，也是众多股市爱好者经常看到的形状。

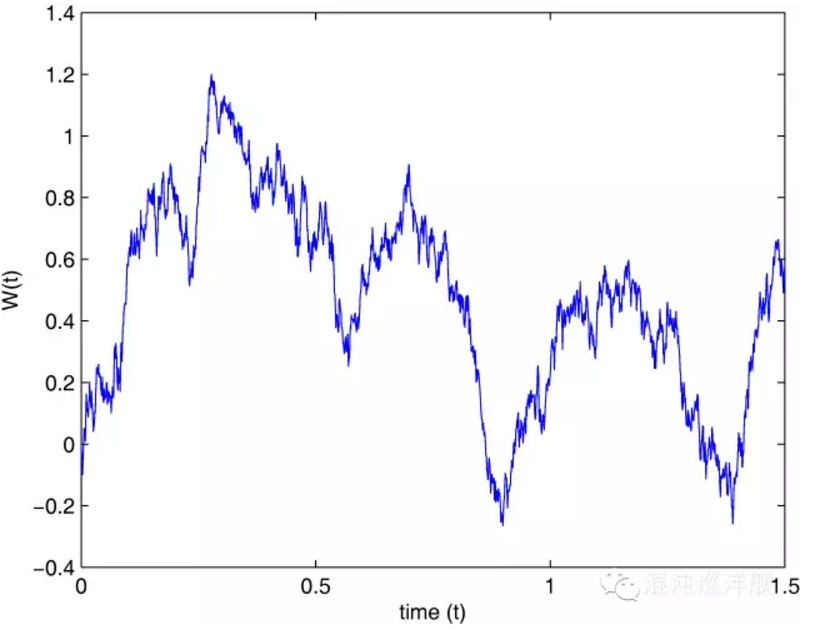
Wiener Process 所依赖的假设特别简单： 醉汉走出的每一步的距离和上一步无关（依然在说马氏性），而这一步走出的长度是由一个确定的高斯分布产生的随机数。 如果这个高斯分布的期望为0，那么这个过程就是一个纯粹的随机游走，反之则是一个但有漂移（drift）的随机游走。

股票和期货等的价格规律，最基本的假设就是随机游走，在此之上可以得到一些简单的定价模型。 但是事实上， 这种规律只在短期内成立，一旦金融危机爆发， 模型就终止了。 而金融危机，依然是过程内部的长程关联的表现。 因为市场的交易毕竟不是随机的，股市的涨落引起人们心情和预期的变化，从而以正反馈的形式给股市，所谓涨则疯买，低则疯卖，这种关联性打破了随机游走的梦。

如何获取信息

说了这么半天随机过程，起核心的应用却还没有谈，如何在一个随机性的变化过程中，提取信息?

首先，变化过程从来都是一些数据记录的，dirty data， 肮脏混乱的数据， 你要把这些data输入到一个电脑程序中，用我说的前面那套东西搞它。随机过程的重要性就在这个数据里提取信息的过程。

怎么搞，分两步，正问题和反问题：

反问题-数据出发：

1. 数据可视化。因为数据杂乱无章，你几乎看不到任何信息，你要做的第一个工作就是让杂乱的数据平均化，平均，才容易观察趋势。那么何为平均化？-低通滤镜，去掉不必要的高频信息。 这里的关键是时间窗口，时间窗口就是你用来作平局的数据尺度，时间窗口内的数据你都用其平均数代替。 时间窗口的选择学问很大，一般越大容易看整体变化的趋势，越小则可以精细统计细节信息。 而最好的做法是在平均时候变化时间窗口，观察数据链是如何随时间窗口大小变化的。

2. 计算分布函数。选择恰当的变量计算分布函数。随机过程的关键信息就在分布函数里。每一种特定的随机过程，都有特定分布函数对应。因此，从分布函数识别随机过程，就是反向判断的关键。

3. 寻找相关性： 信息就是那些多次重复中随机过程中不变的数据信息。所以提取信息首先要足够数据。然后计算不同次试验数据之间的相关性，相关性大小是数据信息含量的直接指示。

4. 统计学习： 基于贝叶斯分析的统计学习将在后续篇章叙述。他是目前从数据里提取信息的大势所趋（state of art）。

正问题-模型出发：

要判断由数据推测出来的随机过程对不对，就反过来进行模型模拟， 模型将产生与试验类似的数据，这个时候我们就可以看我们猜测的模型正确了多少。 比如刚才说的泊松过程就是最简单的模型。 往往我们可以先假定一个过程是泊松过程，然后就可以推得一组分布函数，把推得的分布函数和实际从数据中观测的分布函数比较，我们就可以知道我们和这个最简单的模型的偏差。 模型也是一个循序渐进不断修正的过程， 这点依然和时下流行的统计学习有关。