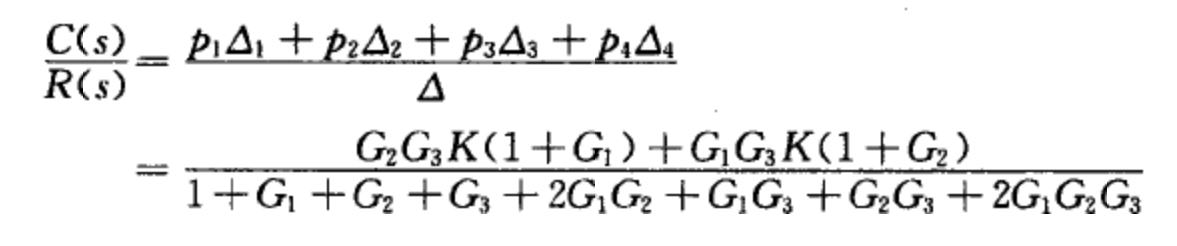跳到主要内容

第二章——控制系统的数学模型

讨论时域和复数域的数学模型

引言​

控制系统的数学模型描述的是系统内部物理量（或变量）之间的数学关系

  • 静态数学模型：描述变量间关系的代数方程
  • 动态数学模型：描述变量各阶导数之间关系的微分方程

目的是对系统做性能分析

模型的建立方法：

  • 分析法：根据物理化学规律等写出相应的运动方程（本章所用方法）
  • 实验法：人为给定输入，记录其输出响应，并用适当的数学模型去逼近

常用的数学模型：（本章研究加粗部分）

  • 时域：微分方程、差分方程、状态方程
  • 复数域：传递函数、结构图
  • 频域：频率特性

2-1 控制系统的时域数学模型​

重点研究线性、定常、集总参量控制系统

1. 线性元件的微分方程​

  • 确定输入和输出
  • 根据物理、化学规律写出微分方程
  • 想去中间变量，得到输出与输入的微分方程

2. 控制系统的微分方程​

  • 由系统原理图画图系统方块图
  • 分别列写各元件的微分方程

可以发现，RLC无源网络和弹簧-质量-阻尼器机械系统的数学模型均是二阶微分方程，我们称这些物理系统为相似系统

3. 线性系统的基本特性​

  • 可叠加性
  • 均匀性

这说明可以把激励单独处理，大大简化了研究

4. 线性定常微分方程的求解​

拉氏变换法

  • 考虑初始条件，对每一项进行拉氏变换，得到关于s的代数式
  • 有代数方程求出拉氏变换函数的表达式
  • 拉氏反变换到的时域方程解

5. 非线性方程的线性化​

切线法

  • 把f(x)在某一点泰勒展开，仅保留一次项
  • 对多变量函数也同样处理
信息

感觉有点像把各个维度解耦了，并且只按切线/切平面来做计算

6. 运动的模态​

如果n阶微分方程的特征根存在，则对应得到的e指数函数解就是微分方程所描述运动的模态，又称振型

每一种模态都代表一种类型的运动状态，齐次微分方程的通解就是模态的线性组合

注意

共轭复模态eσ+jωe^{\sigma+j\omega}和eσ−jωe^{\sigma-j\omega}可以写成实函数模态eσtsinωte^{\sigma t}sin\omega t与eσtcosωte^{\sigma t}cos\omega t的形式

2-2 控制系统的复数域数学模型​

传递函数非常重要，是根轨迹、频率法的基础，同时还可以研究结构变化对系统性能的影响

1. 传递函数的定义和性质​

==定义==

  • 线性定常系统的传递函数，定义为零初始状态下，系统输出量的拉氏变换与输入量的拉氏变换之比

==性质==

  • 传递函数是复变量s的有理真分式，具有复变函数的所有性质
  • 传递函数值取决于系统和元件的结构与参数，与输出量无关
  • 传递函数与微分方程有相通性s→ddts\rightarrow \frac{d}{dt}
  • 传递函数G(s)的反变换为脉冲响应h(t)

2. 传递函数的零点和极点​

略

3. 传递函数零极点对输出的影响​

传递函数极点——微分方程的特征根——决定了系统自由运动的模态——强迫运动中也会包含这些自由运动的模态

如

G(s)=C(s)R(s)=6(s+3)(s+1)(s+2)G(s)=\frac{C(s)}{R(s)}=\frac{6(s+3)}{(s+1)(s+2)}

自由运动的模态是e−te^{-t}和e−2te^{-2t}

当r(t)=R1+R2e−5tr(t)=R_1+R_2e^{-5t}时

c(t)=L−1[C(s)]=L−1[6(s+3)(s+1)(s+2)(R1s+R2s+5)]=9R1−R2e−5t+(3R2−12R1)e−t+(3R1−2R2)e−2t\begin{aligned} c(t) & =\mathscr{L}^{-1}[C(s)] \\ & =\mathscr{L}^{-1}\left[\frac{6(s+3)}{(s+1)(s+2)}\left(\frac{R_1}{s}+\frac{R_2}{s+5}\right)\right] \\ & =9 R_1-R_2 \mathrm{e}^{-5 t}+\left(3 R_2-12 R_1\right) \mathrm{e}^{-t}+\left(3 R_1-2 R_2\right) \mathrm{e}^{-2 t} \end{aligned}

式中，前两项具有与输入函数 r(t)r(t) 相同的模态，后两项中包含了由极点 -1 和 -2 形成的自由运动模态。这是系统“固有” 的成分，但其系数却与输入函数有关，因此可以认为这两项是受输入函数激发而形成的。

传递函数的极点可以受输入函数的激发，在输出响应中形成自由运动的模态。

传递函数的零点并不形成自由运动的模态，但是他们影响模态在响应中的比重

零点如果距离原点远、离极点近，则对应模态所占比重就小

4. 典型元部件的传递函数​

  • 电位计
    • 负载效应
  • 测速发电机
  • 电枢控制直流伺服发电机
  • 两相伺服电动机
  • 无源网络
    • 可能需要考虑负载效应（两个电路直接链接器传递函数不是简单相乘）
    • C的复阻抗为1Cs\frac{1}{Cs}，L的复阻抗为Ls
  • 单容水槽（一阶过程）
  • 电加热炉（一阶过程）
  • 有纯延迟的单容水槽（多了延时因子）
  • 双容水槽（二阶过程）

2-3 控制系统的结构图和信号流图​

1. 系统结构图的组成和绘制​

四种基本单元

  • 信号线
  • 引出点（测量点）
  • 比较点（综合点）
  • 方框（环节）

2. 结构图的等效变换和简化​

这个过程对应于方程消去中间变量求系统传递函数的过程

  • 串并联

  • 反馈

    • 负号对应正反馈，正号对应负反馈
Φ(s)=G(s)1∓G(s)H(s)\Phi(s)=\frac{G(s)}{1 \mp G(s) H(s)}

3. 信号流图的组成和性质​

信号流图起源于梅森用图示法来描述一个或一组线性代数方程式，它是有节点和支路组成的一种信号传递网络

备注

只有节点和支路两种成分，而结构图有四种基本单元

性质：

  • 节点标志系统的变量
  • 支路相当于乘法器
  • 信号在支路上只能沿单箭头传递
  • 给定系统的信号流图不是唯一的

名词术语

  • 源节点（输入节点）/陷节点（输出节点）
  • 混合节点
  • 前向通路——信号从输入节点到输出节点传递时，每个节点只通过一次的通路
    • 前向通路增益——PkP_k
  • 回路——起点和终点在同一节点，而且信号通过每一节点不多于一次的闭合通路
    • 回路增益——LaL_a
  • 不接触回路——回路之间没有公共节点

4. 信号流图的绘制​

  • 从系统微分方程——每个变量指定一个节点
  • 从结构图——把传递的信号用小圆圈表示
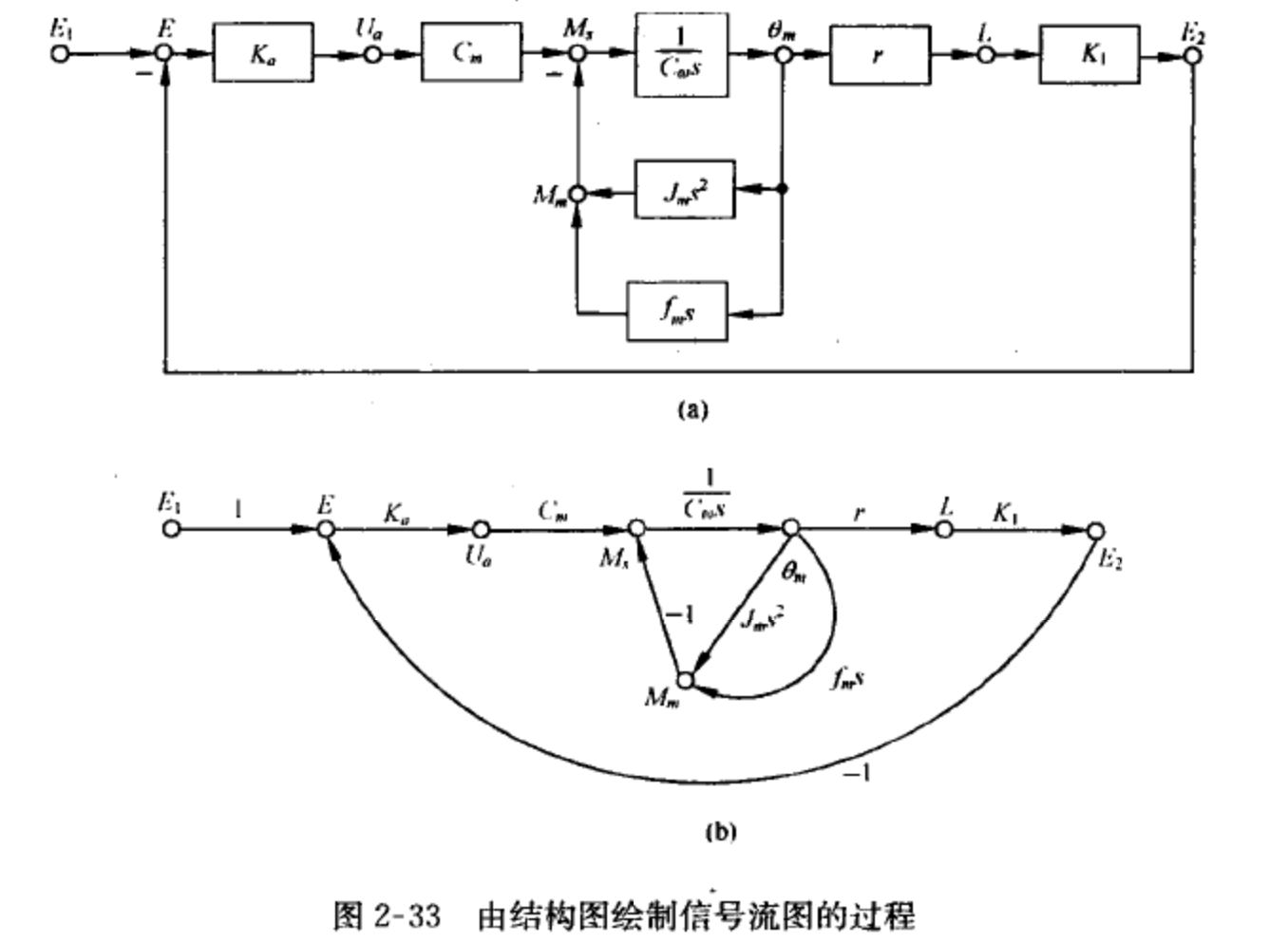
image-20230611192535418
  • 信号流图的简化

支路增益为1（-1）的相邻两个节点，一般可以合并为一个节点，上图中的MsM_s和MmM_m可以合并成一个节点，变量是Ms−MmM_s-M_m

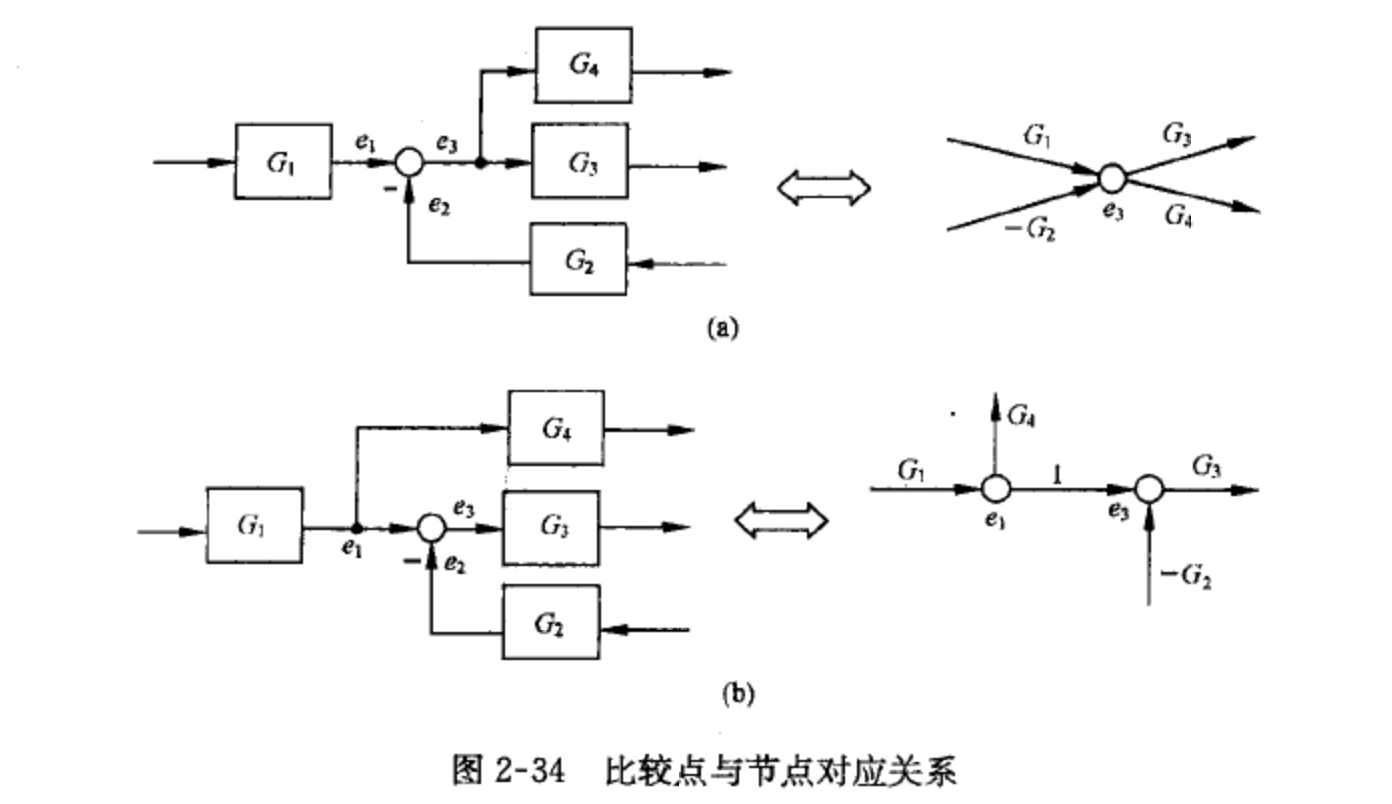
image-20230611192941321

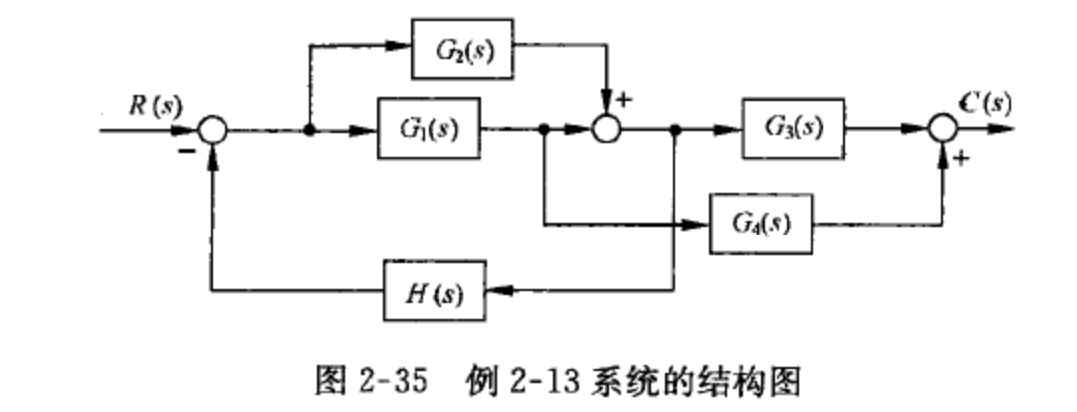
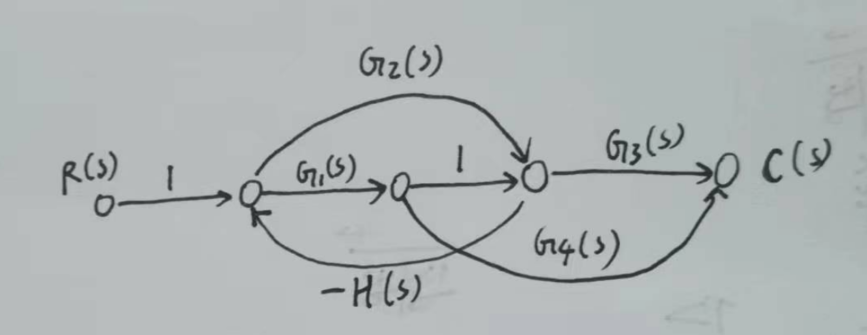
例：绘制下述系统结构图的信号流图

image-20230611193459056

可以先按顺序画出中间通路，再补齐上下的分支

image-20230611194343927

5. 梅森增益公式​

本质上是应用了克莱姆法则求解方程组，表述为

P=1Δ∑k=1npkΔkP=\frac{1}{\Delta} \sum_{k=1}^n p_k \Delta_k

其中分母多项式为：

Δ=1−∑Lu+∑LbLc−∑LdLeLf+⋯\Delta = 1-\sum L_u+\sum L_b L_c-\sum L_d L_e L_f+\cdots
  • ∑La\sum L_a 表示信号流图中所有单独回路的回路增益之和项
  • ∑LbLc\sum L_b L_c 表示信号流图中每两个互不接触的回路增益之乘积的和项
  • ∑LdLeLf\sum L_d L_e L_f 为所有互不接触的单独回路中，每次取其中三个回路的回路增益的乘积之和

分子中

  • pkp_k 是第 kk 条前向通路总增益
  • Δk\Delta_k 是与第 kk 条前向通路对应的余因子式
    • 等同系数行列式Δ\Delta中去掉与第kk条前向通路接触的所有回路的回路增益项之后的余子式

例：

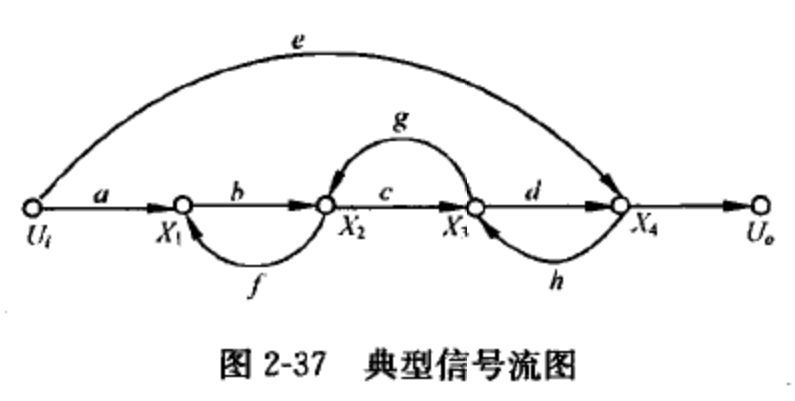
image-20230611195934955
image-20230611201450611

例：

image-20230611201511925
提示

先画流图，再计算

image-20230611201532734

例：

求X4/X1和X2/X1

image-20230611201556889

X4/X1：

image-20230611201632036

X2/X1：

注意

求X2/X1的时候仍然是一样的用法

image-20230611201643630

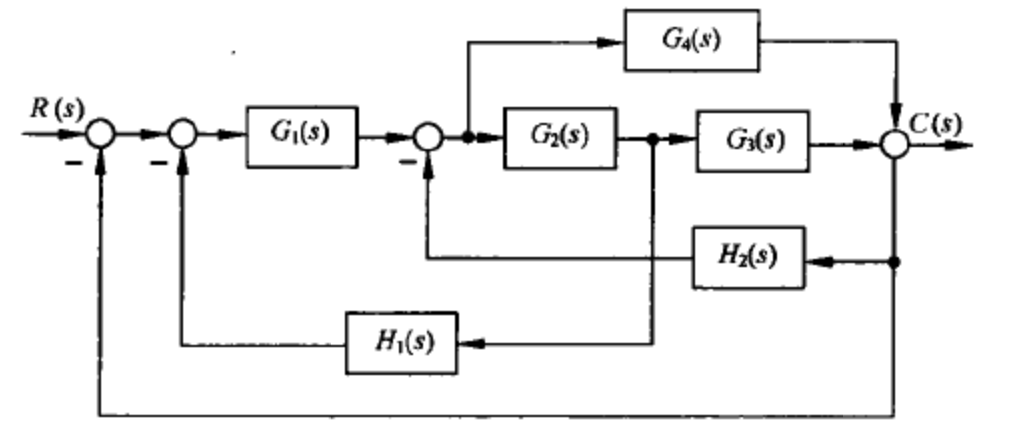
例：

image-20230611202126827
注意

这里有四个回路，且存在三个回路互不相交，所以有∑LdLeLf\sum L_d L_e L_f项

image-20230611202223660

6. 闭环系统的传递函数​

有时候我们需要研究扰动N(s)N(s)对系统输出C(s)C(s)的影响，或是以误差E(s)E(s)为输出量，所以我们在画流图的时候可以画多个源节点或陷节点：

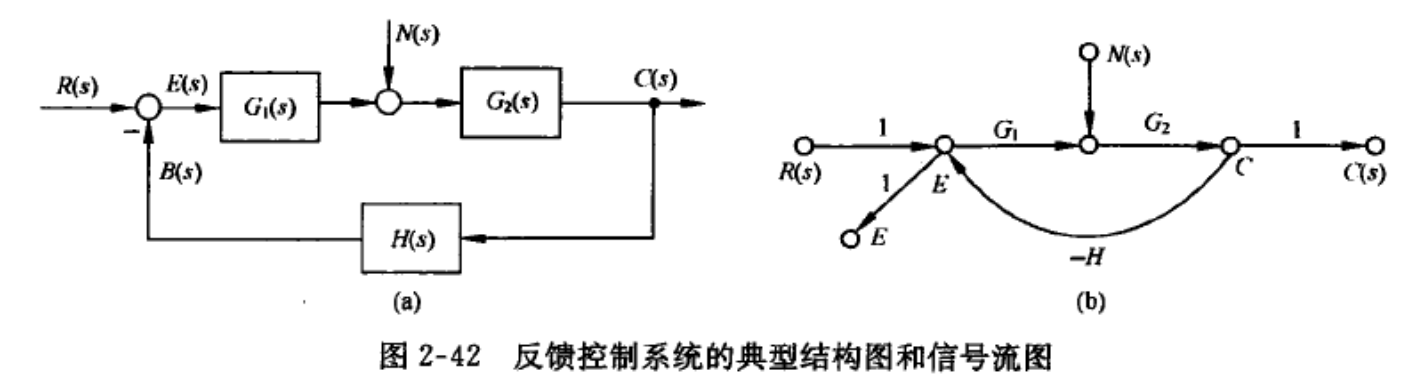
image-20230611202719389

（1）输入信号作用下的闭环传递函数（以R(s)R(s)作输入）

Φ(s)=C(s)R(s)=G1(s)G2(s)1+G1(s)G2(s)H(s)\Phi(s)=\frac{C(s)}{R(s)}=\frac{G_1(s) G_2(s)}{1+G_1(s) G_2(s) H(s)}

（2）扰动作用下的闭环传递函数（以N(s)N(s)作输入）

Φn(s)=C(s)N(s)=G2(s)1+G1(s)G2(s)H(s)\Phi_n(s)=\frac{C(s)}{N(s)}=\frac{G_2(s)}{1+G_1(s) G_2(s) H(s)}

（3）输入和扰动同时作用下的系统输出（叠加原理）

∑C(s)=Φ(s)⋅R(s)+Φn(s)⋅N(s)=11+G1(s)G2(s)H(s)[G1(s)G2(s)R(s)+G2(s)N(s)]\begin{aligned} \sum C(s) & =\Phi(s) \cdot R(s)+\Phi_n(s) \cdot N(s) \\ & =\frac{1}{1+G_1(s) G_2(s) H(s)}\left[G_1(s) G_2(s) R(s)+G_2(s) N(s)\right] \end{aligned}

上式如果满足 ∣G1(s)G2(s)H(s)∣≫1\left|G_1(s) G_2(s) H(s)\right| \gg 1 和 ∣G1(s)H(s)∣≫1\left|G_1(s) H(s)\right| \gg 1 的条件, 则可简化为

∑C(s)≈1H(s)R(s)\sum C(s) \approx \frac{1}{H(s)} R(s)
注意

此时，系统的输出值只取决于反馈通路传递函数H(s)H(s)和输入信号R(s)R(s)

既与前向通路传递函数无关, 也不受扰动作用的影响。【深度负反馈】

特别是当 H(s)=1H(s)=1, 即单位反馈时, C(s)≈R(s)C(s) \approx R(s), 从而近似实现了对输人信号的完全复现, 且对扰动具有较强的抑制能力。

（4）闭环系统的误差传递函数

Φe(s)=E(s)R(s)=11+G1(s)G2(s)H(s)\Phi_e(s)=\frac{E(s)}{R(s)}=\frac{1}{1+G_1(s) G_2(s) H(s)}
Φen(s)=E(s)N(s)=−G2(s)H(s)1+G1(s)G2(s)H(s)\Phi_{e n}(s)=\frac{E(s)}{N(s)}=\frac{-G_2(s) H(s)}{1+G_1(s) G_2(s) H(s)}
提示

注意到本例中各种闭环系统传递函数的分母形式均相同，这是因为它们都是同一个信号流图的特征式，即Δ=1+G1(s)G2(s)H(s)\Delta=1+G_1(s) G_2(s) H(s), 式中 G1(s)G2(s)H(s)G_1(s) G_2(s) H(s) 是回路增益，上述系统的开环传递函数, 它等效为主反馈断开时，从输入信号 R(s)R(s) 到反馈信号 B(s)B(s) 之间的传递函数（只断开反馈，但是不删除下面的H(s)H(s)）

编辑此页
最后由 xiaofan4122 于 更新