刚体火箭控制器设计
四个火箭姿控的性能指标
他们相互联系、互相制约
- 稳定性指标
- 绝对稳定性——极点位置
- 相对稳定性——动态特性品质和裕度
- 动态性能指标
- 过渡时间、超调量、振荡次数满足要求
- 跟踪精度指标
- 满足小扰动条件
- 抗干扰指标
- 低频干扰——补偿、抵消
- 高配干扰——抑制、衰减
姿态控制器设计
设计策略——基于误差来消除误差,采用线性框架下的PID控制
仅仅一个P会使系统有较大振荡(虽然稳定了)
引入D(微分控制),消除振荡,但存在稳态误差
引入I(积分控制),将系统由二阶系统改造为一阶系统,对阶跃指令无稳态误差(不过积分会降低相位裕度)
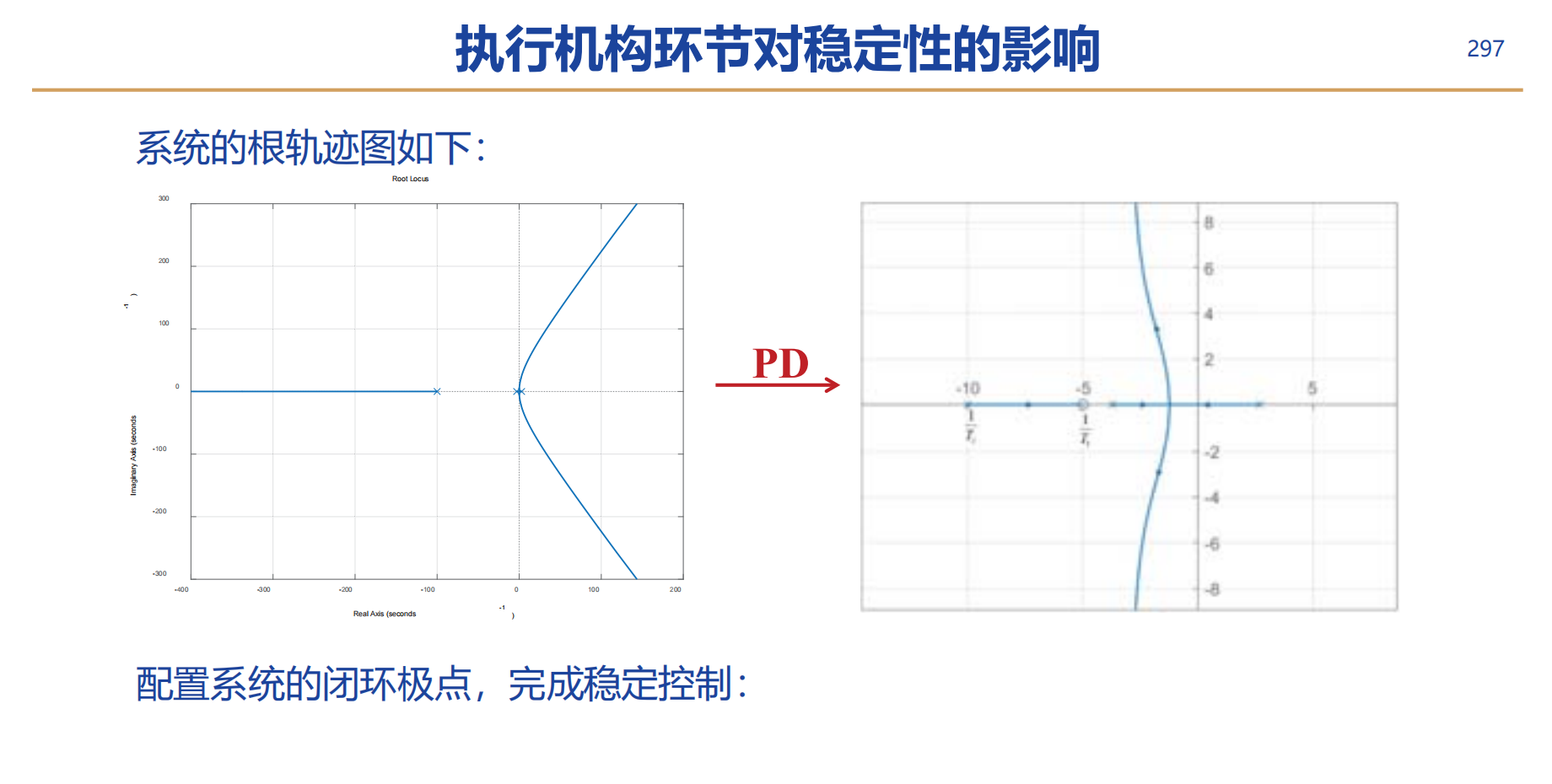
复合控制:反馈加前馈
在反馈的基础上添加前馈回路,可以减小稳态控制误差,不影响系统稳定性
风干扰误差,可以通过PD->PID消除,也可以通过前馈消除
风干扰可以通过前馈完全补偿,但是可能会导致箭体内部载荷过大而使箭体折断,因此只能补偿一部分风干扰
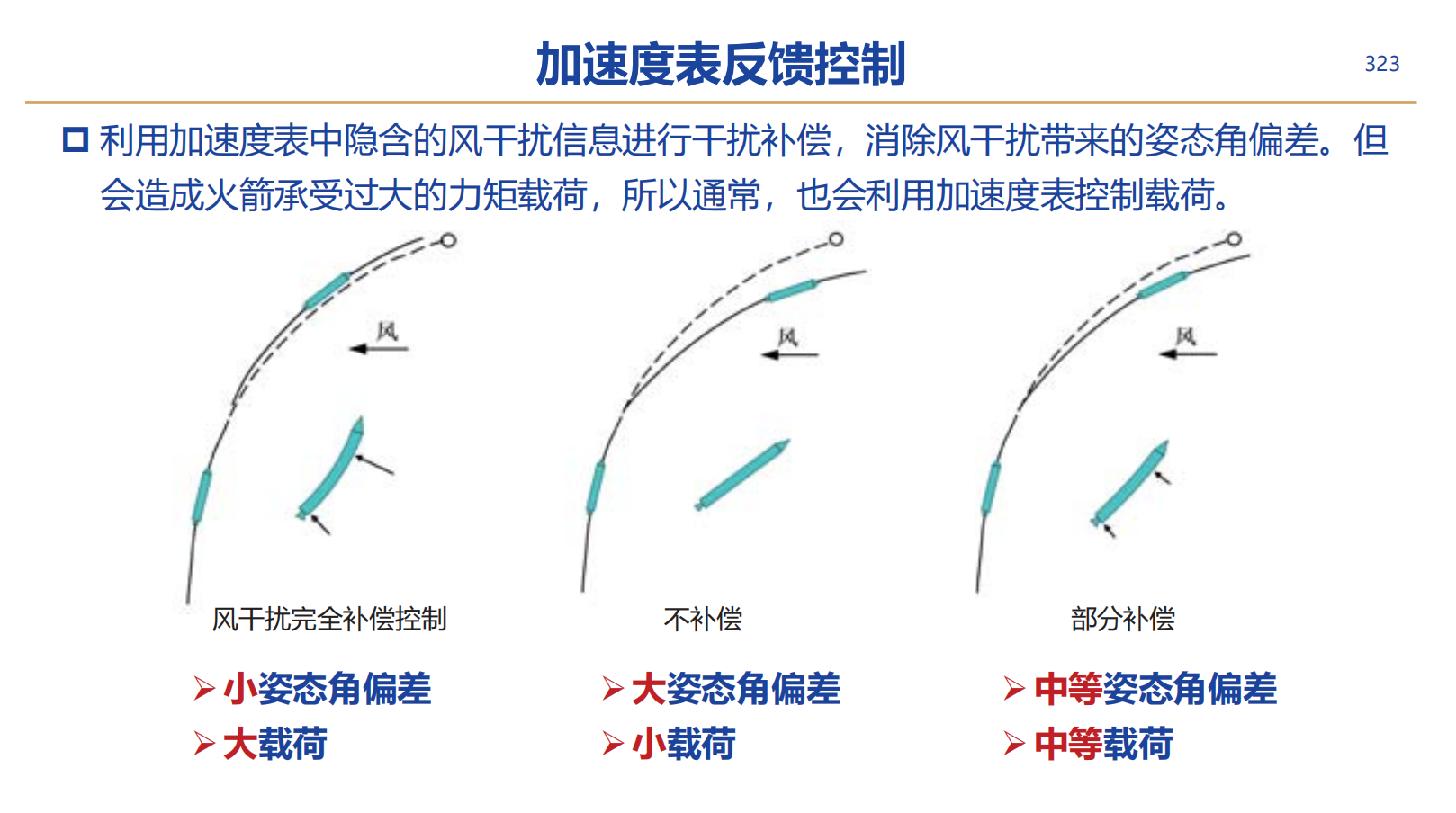
但是前馈控制只能补偿这种有模型的误差,去掉积分环节会使其他的很多干扰不能补偿
可以通过控制回路中增加扩张状态观测器,对干扰进行在线估计,然后消除估计出的干扰力矩
姿控系统的鲁棒性
鲁棒性指标
当参数(或结构)存在某种程度的不确定性时,系统仍能保证稳定性
- 稳定裕度(SM)奈奎斯特曲线到临界点(-1,0)的最短距离
- 幅值裕度(GM)在闭环系统变得不稳定之前,环路传递函数的增益可以增加的最大值,是奈奎斯特曲线与x轴负方向交点对应幅值的倒数
- 相位裕度(PM)在闭环系统变得不稳定之前,环路传递函数的相位滞后量,是系统截止频率对应的相角距离-180°的相位差
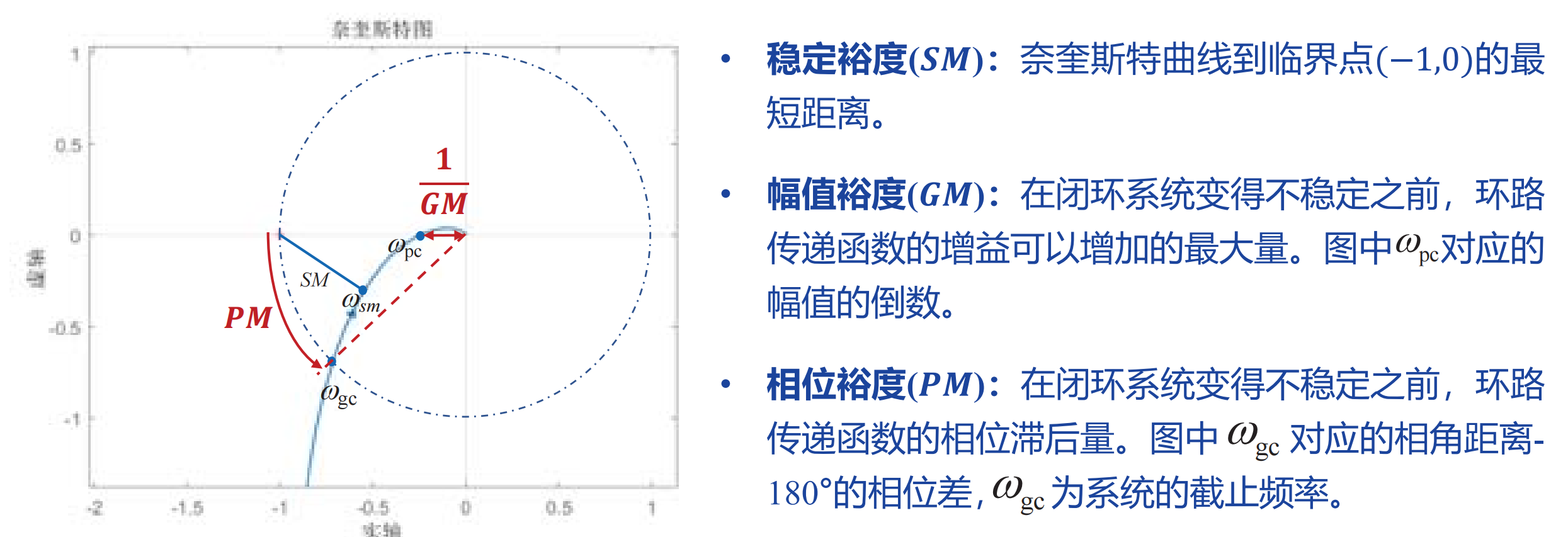
良好的系统相位裕度在40°左右,幅值裕度应该大于6dB
灵敏度函数
可以表示反馈(闭环)对开环的影响,他即是稳态误差的度量,也是抗扰性的度量
灵敏度极大值越大,系统稳定裕度越低
灵敏度极大值越小,其各项指标也越优异,但是灵敏度的最小值也有(可用带宽)限制
可用带宽
高带宽一般意味着高成本,对于有限带宽的系统,其灵敏度函数满足伯德积分
如果干扰衰减在一个频段上得到了改善,那么 他必然会在另一个频段上变差
系统的可用带宽增加,敏感度极大值下降,稳定裕度增加
根据经验,可用带宽是不稳定极点的十倍以上