摄动制导
前面我们简要介绍了火箭主动段的流程和制导方法,理论上火箭在关机点关机后不再需要控制,可以在重力作用下滑行至自由段结束,但是总是存在一些误差,所以我们在主动段快要结束时需要修正这个弹道,使得关机点满足我们的需求。
下面这个方程称为关机方程
F(r,v,rT)=0 其中r,v,rT分别是位矢、速度矢量、目标点位矢,关机点理应满足这个方程
显然关机点的状态不是唯一的(如下图),那么如何设计关机方程呢
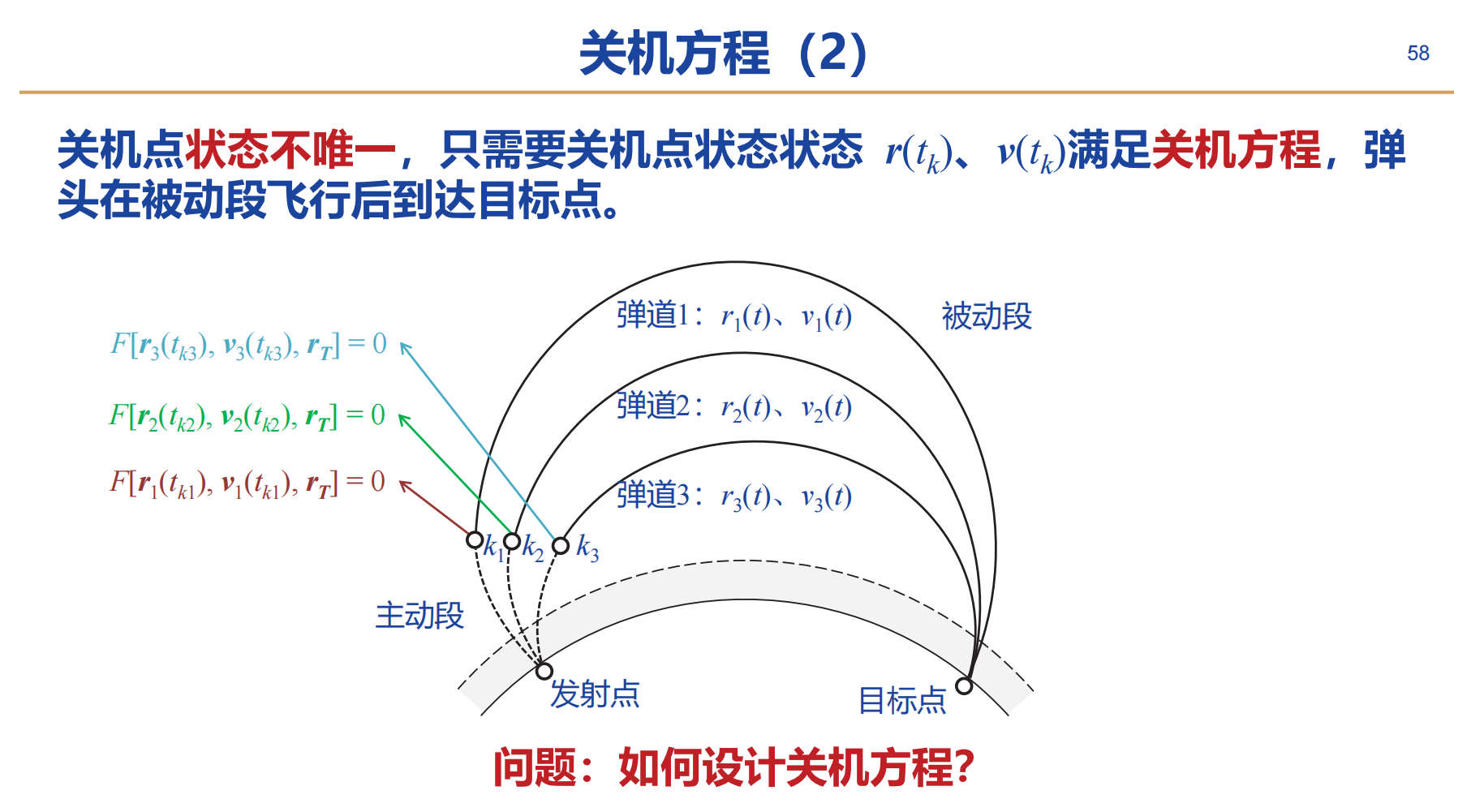
因为关机点存在偏差,所以关机点实际状态预测出的落点会和目标落点存在一定的偏差,不考虑地球自转,忽略被动段气动力和重力异常等因素,射程偏差可以定义为弹目距离-预估射程
ΔL(rk,vk,rT)=Lˉ(rk,rT)−L(rk,vk) 我们的目标就是让这个偏差为0
ΔL[r(tk),v(tk),rT]=0 但是我们并不知道这个函数具体是什么
一般来说,我们可以先设计一条弹道,然后假设主动段整个导弹的实际弹道和标称弹道相差不大,那么我们就可以将关机方程在标称关机点做一阶泰勒近似,得到标称关机点射程偏差的表达式
ΔL(1)[X(t)]=∂Xˉ(tˉk)∂ΔL[X(t)−Xˉ(tˉk)] 其中
X(t)=[rT(t)vT(t)]T 他包含了导弹的位置、速度信息
这个相当于把偏差线性化了,最终的偏差认为是斜率(偏导)乘以dx(状态偏差),得到的就是射程偏差
首先需要在发射前离线计算并存储Xˉ(tˉk),∂Xˉ(tˉk)∂ΔL,他们分别代表导弹在标称时间的状态信息(位置和速度)以及射程偏差对状态的偏导
导弹点火起飞后,在主动段飞行的前半段,导弹会按照标称弹道飞行,实际弹道在标称弹道附近
接近标称关机点时,制导系统开始计算关机方程,并且根据关机方程的偏差设计导引方程,调整姿态角
只有在关机方程满足时,制导系统才会发出关机指令
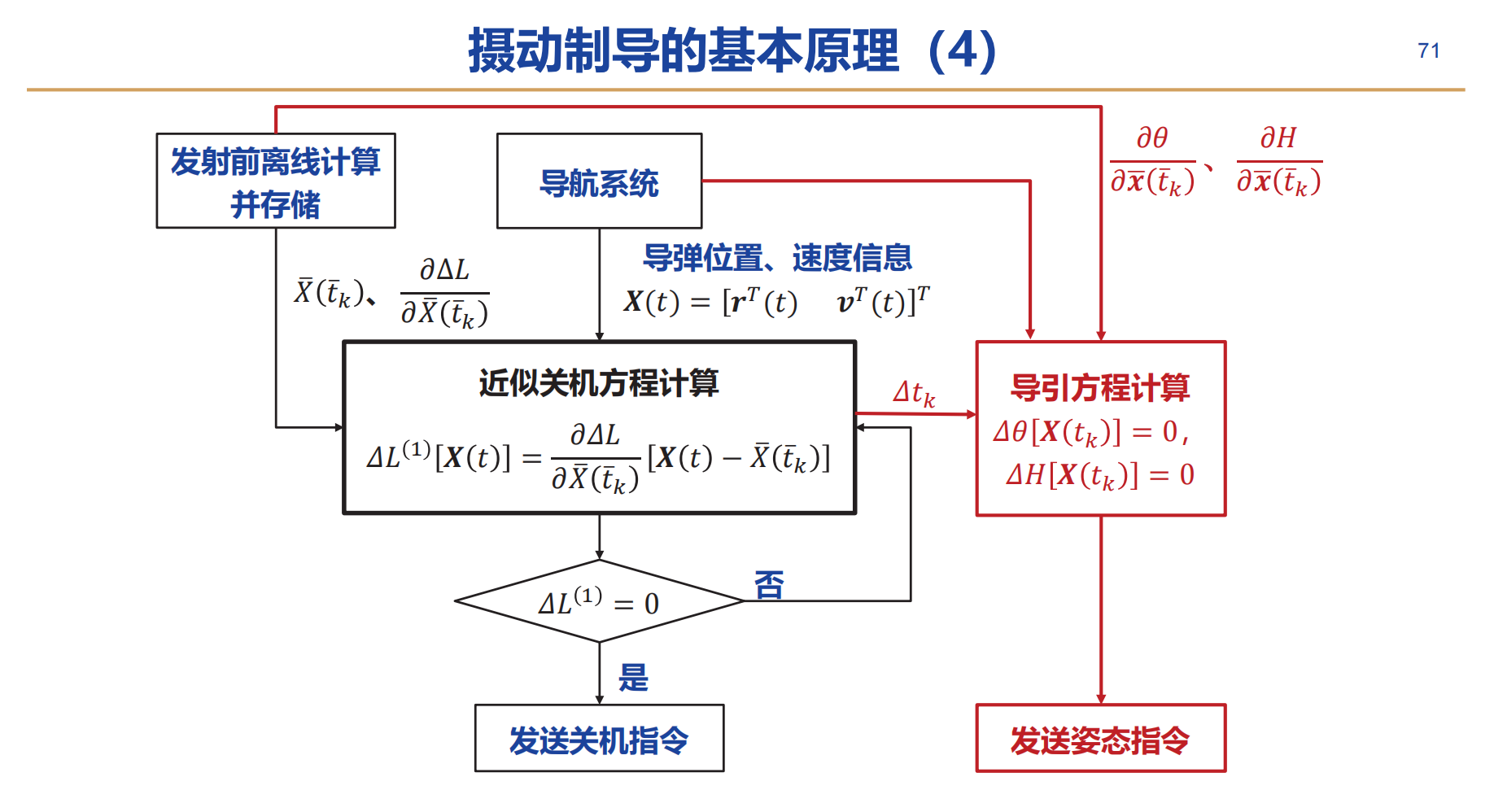
上图中黑色和蓝色部分是射程偏差的计算框图,其偏差信息回输入到导引方程中,并且调整火箭姿态,最终使得关机方程满足
在大的建模误差和外扰下,一阶线性近似方程不能准确描述非线性关机方程
全偏差等于等时偏差加上时间不一致导致的偏差

