跳到主要内容

闭环制导

主要是主动段后半程，大气层外的制导律

基础知识​

闭环制导与摄动制导区别​

  • 摄动制导——对姿态角、发动机关机时间进行离线设计
  • 闭环制导——在简化条件下，得到运动方程的显式解（解析或数值）基于制导误差进行全量反馈调节

大气层内外制导不同​

  • 大气层内——气动力影响显著，重力场影响小
  • 大气层外——气动力影响小，重力场影响显著
说明

接下来我们讨论的都是主动端后半程，大气层外的制导，需要的一个最重要的运动方程是

dvdt=Fpm+g\frac{\mathrm{d} \boldsymbol{v}}{\mathrm{d} t}=\frac{\boldsymbol{F}_p}{m}+\boldsymbol{g}

该方程可以写为如下的形式：

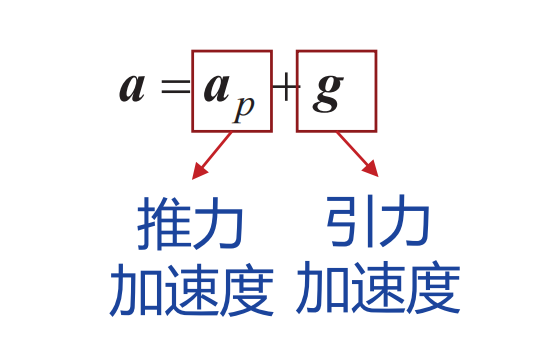
image-20230615165708465

需要速度与待增速度​

在当前位置矢量r(t)r(t)处，如果以需要速度vR(t)v_R(t)关机，可以完成制导任务

注意

在本课程中，需要速度是当前位置矢量与当前时间的函数

这是因为只要我们确定了物体的位置，那么显然他关机后会自由滑行，其运动方程会非常简单，很容易反向确认出初速度（也就是此时的需要速度），不过我们知道从一点抛到另一点的轨迹有无数条，所以一般会加一些约束条件

待增速度就是需要速度与当前速度之差

导引方法​

导引目标​

下面两个目标实际上是等效的

  • 将当前速度导引至需要速度
  • 将待增速度导引至0

之后的讨论中我们使用第二种定义

三种导引策略​

这里我们假设待增速度vgav_{ga}是已知的，来确定发动机推力FpF_p的大小和方向

导引策略1（他甚至不配拥有名字）

加速度方向与待增速度方向相同

a×vga=0a\times v_{ga}=0

当推力远大于引力时，也可以写为

ap×vga=0a_p\times v_{ga}=0

导引策略2——叉积导引

待增速度导数负方向与待增速度方向相同

v˙ga×vga=0\dot v_{ga}\times v_{ga}=0

这里涉及到的待增速度变化率，他可以写成需要速度的变化率减去当前速度的变化率

v˙ga=v˙R−v˙=v˙R−g−ap\dot{\boldsymbol{v}}_{g a}=\dot{\boldsymbol{v}}_R-\dot{\boldsymbol{v}}=\dot{\boldsymbol{v}}_R-\boldsymbol{g}-\boldsymbol{a}_p

令

p=v˙R−g\boldsymbol{p}=\dot{\boldsymbol{v}}_R-\boldsymbol{g}

则

(p−ap)×vga=0\left(\boldsymbol{p}-\boldsymbol{a}_p\right) \times \boldsymbol{v}_{g a}=0
注意

那么新问题出现了，怎样求需要速度的变化率？

导引策略3——结合1、2的方式

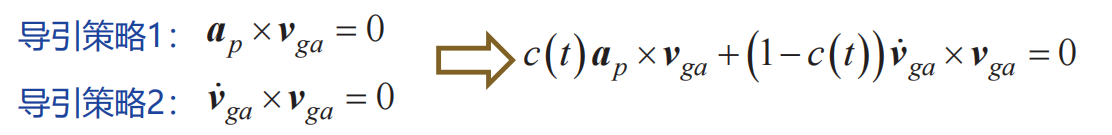
image-20230615164447212

3种导引策略对比

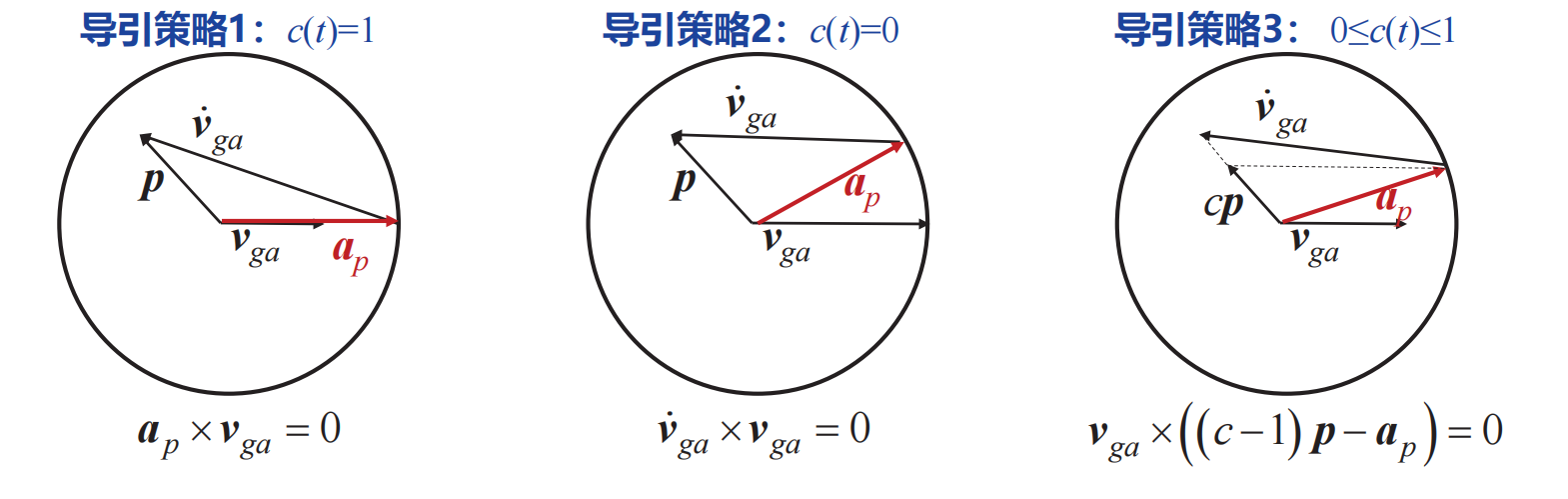
image-20230615171145975

需要速度的计算​

在上面的两种制导方式中，我们发现都需要知道需要速度及其导数，总体上有两种方法确定

Lambert制导​

关于兰伯特问题的说明参见这里：兰伯特问题 - 卫星百科

标准的兰伯特问题被描述为：给定初末位置和转移时间，求初末速度。这正好符合我们的条件，因为我们在设计轨道时，限定了再入点，而需要速度的定义就是当前时刻关机，那么当前位置就是关机点，然后再给定一个目标时间就可以利用Lambert制导求出飞行器当前需要速度了。

说明

在上面那个链接里说，Lambert问题是没有解析解的，但是在老师的PPT里却说可以求出Lambert问题的闭环解析解，最终的形式是把速度大小、速度倾角、需要时间表示成了相应的函数，这里并没有指定目标时间，也许这就是能得到解析解的原因？

现在最大的疑惑就是怎么实时而又快速的计算Lambert方程，得到现在的需用速度，按理来说，目标时间tFt_F应该也是输入变量才对，

Q制导​

Q制导里首先就假定了需要速度就只是当前位置和时间的函数，然后就可以写成vR(r(t),t)\boldsymbol{v}_R(\boldsymbol{r}(t), t)的形式

注意到其中矢径也是时间t的函数，所以对t求导时是复合函数求导，同时需要求偏导：

dvR dt=∂vR∂t+∂vR∂rdrdt\frac{\mathrm{d} \boldsymbol{v}_R}{\mathrm{~d} t}=\frac{\partial \boldsymbol{v}_R}{\partial t}+\frac{\partial \boldsymbol{v}_R}{\partial \boldsymbol{r}} \frac{\mathrm{d} \boldsymbol{r}}{\mathrm{d} t}

上面的式子又可以化成

上式=∂vR∂t+∂vR∂rv=∂vR∂t+∂vR∂r(vR−vga)=g−∂vR∂rvga上式=\frac{\partial \boldsymbol{v}_R}{\partial t}+\frac{\partial \boldsymbol{v}_R}{\partial \boldsymbol{r}} \boldsymbol{v}=\frac{\partial \boldsymbol{v}_R}{\partial t}+\frac{\partial \boldsymbol{v}_R}{\partial \boldsymbol{r}}\left(\boldsymbol{v}_R-\boldsymbol{v}_{g a}\right)=\boldsymbol{g}-\frac{\partial \boldsymbol{v}_R}{\partial \boldsymbol{r}} \boldsymbol{v}_{g a}

这一块还比较绕，位矢的时间导数首先换成当前速度，然后再换成需用速度减待增速度，最后一步中：

∂vR∂t+∂vR∂rvR=g\frac{\partial \boldsymbol{v}_R}{\partial t}+\frac{\partial \boldsymbol{v}_R}{\partial \boldsymbol{r}} \boldsymbol{v}_R=\boldsymbol{g}

这是因为当前速度等于需要速度时，发动机关机，待增速度为0，飞行器就仅受重力作用，速度变化率就等于重力加速度：

dvdt=∂vR∂rvR+∂vR∂t=g\frac{\mathrm{d} \boldsymbol{v}}{\mathrm{d} t}=\frac{\partial \boldsymbol{v}_R}{\partial \boldsymbol{r}} \boldsymbol{v}_R+\frac{\partial \boldsymbol{v}_R}{\partial t}=\boldsymbol{g}

前面已经说了待增速度导数与需要速度导数之间的关系，他等于需要速度的变化率减去当前速度的变化率

v˙ga=v˙R−v˙=v˙R−g−ap\dot{\boldsymbol{v}}_{g a}=\dot{\boldsymbol{v}}_R-\dot{\boldsymbol{v}}=\dot{\boldsymbol{v}}_R-\boldsymbol{g}-\boldsymbol{a}_p

把需要速度的变化率带入其中得

dvga dt=dvR dt−g−ap=g−∂vR∂rvga−g−ap=−∂vR∂rvga−ap\frac{\mathrm{d} \boldsymbol{v}_{g a}}{\mathrm{~d} t}=\frac{\mathrm{d} \boldsymbol{v}_R}{\mathrm{~d} t}-\boldsymbol{g}-\boldsymbol{a}_p=\boldsymbol{g}-\frac{\partial \boldsymbol{v}_R}{\partial \boldsymbol{r}} \boldsymbol{v}_{g a}-\boldsymbol{g}-\boldsymbol{a}_p=-\frac{\partial \boldsymbol{v}_R}{\partial \boldsymbol{r}} \boldsymbol{v}_{g a}-\boldsymbol{a}_p

定义Q矩阵为需要速度对位矢的偏导

Q=∂vR∂r\boldsymbol{Q}=\frac{\partial \boldsymbol{v}_R}{\partial \boldsymbol{r}}

则待增速度的导数为：

dvga dt=−Qvga−ap\frac{\mathrm{d} \boldsymbol{v}_{g a}}{\mathrm{~d} t}=-\boldsymbol{Q} \boldsymbol{v}_{g a}-\boldsymbol{a}_p
巧记

这里写成了状态空间的形式，类似与x˙=Ax+bu\dot x=Ax+bu，这里xx就是待增速度，AA就是−Q-Q，b就是-1，u是apa_p

其框架图为

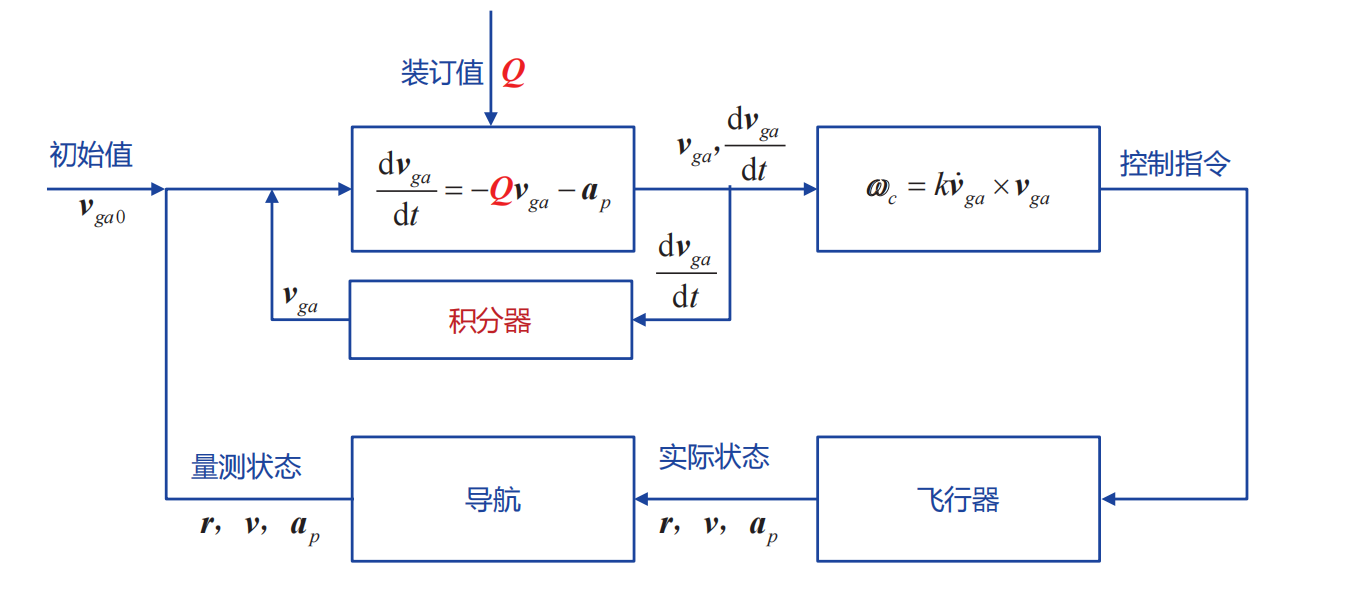
image-20230615184315071

Q制导补充说明​

  • Q矩阵是可离线计算的时变矩阵
  • 通过Q矩阵计算，隐式的依赖重力场
  • apa_p是发动机推力加速度，加速度计直接测量【注意这一个，制导并不控制apa_p大小，只对方向控制】
  • 对上式积分，可以得到vgav_{ga}
  • 时变矩阵Q的存储和运算是困难的，因此其应用场景主要为：当主动段地心转角比较小时，可将Q矩阵视为常值矩阵
  • 在任意时间t，为了最小化发动机剩余燃烧时间，应当最大化ap⋅vgaa_p·v_{ga}，即采取第一种导引策略
编辑此页
最后由 xiaofan4122 于 更新