火箭姿态稳定性分析

箭控系统组成，系数冻结法在三个特殊点运用，发现都不稳定

基础知识

箭控系统的基本组成

制导指令输入控制器中，控制器控制执行机构，进而控制发动机推力、摆角等，输出会有传感器采集参数，然后反馈到控制器中

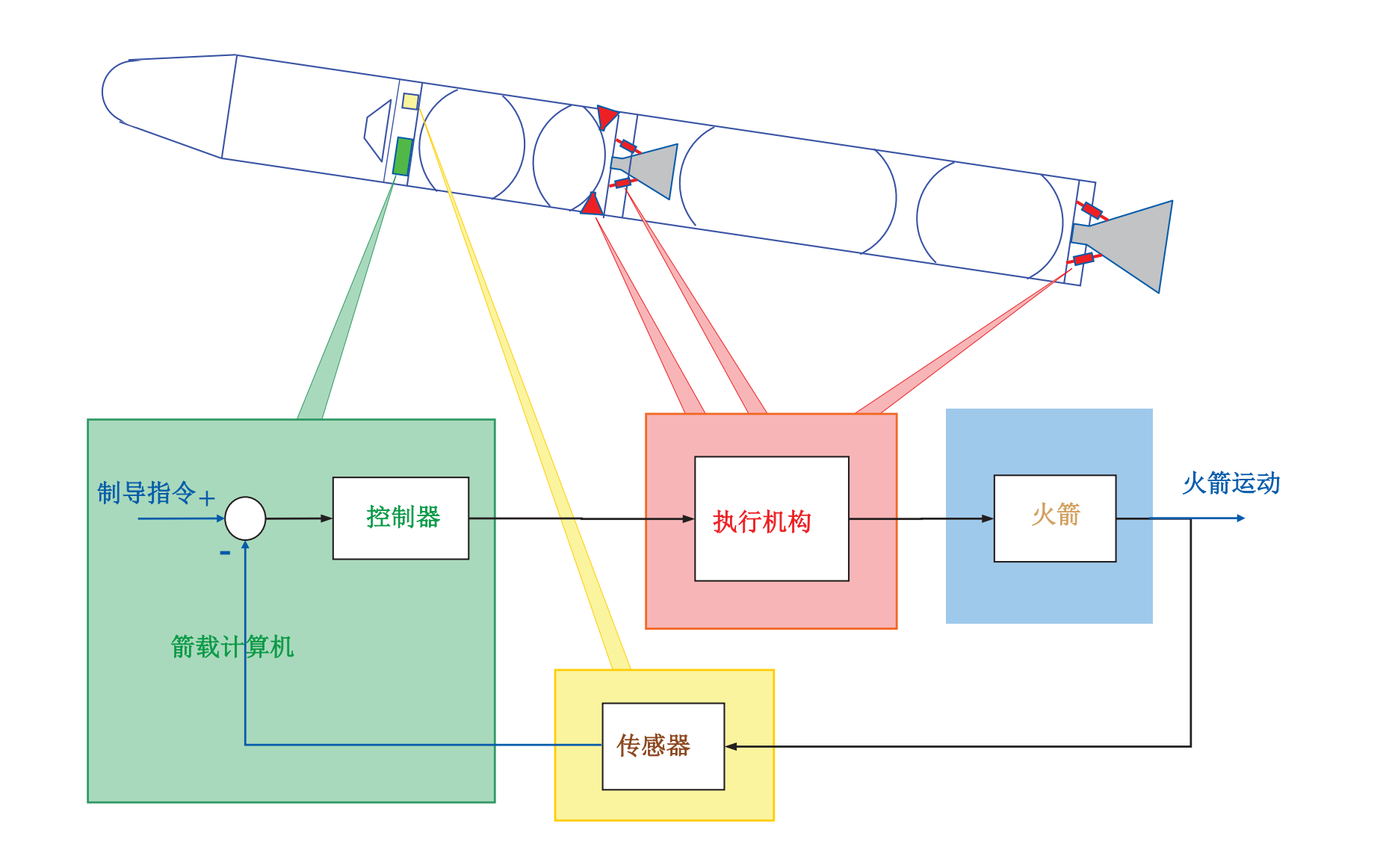
火箭绕质心运动

• 刚体运动
• 推进剂晃动
• 弹体弹性振动

火箭姿态动力学特点

1. 运载火箭动力学模型复杂、阶次高
2. 特性参数时变
3. 飞行环境负载且存在干扰与不确定性
4. 结构刚度低、低频特性可能存在耦合（液体晃动、弹性）

火箭姿控控制任务

前提条件：不能调节推力大小，主要靠控制弹体的推力方向

而弹体的推力方向由姿态角决定，

所以姿控系统的任务就是“根据制导和导航系统提供的信号”控制刚性弹体的姿态角

稳定性

• 李雅普诺夫稳定
• 线性系统稳定——极点全部在左半平面
• 采用系数冻结法判断稳定性

有干扰作用的飞行器姿态运动方程的系数是时变的，但是绕质心运动发暂态过程比线性时变系统的系数变化快，因此可以认为在某一短时间内，方程系数不变化，而将姿态运动方程视为常微分方程

火箭的线性化模型

三通道解耦、小角度假设

• 若气动压心在质心之前，即$b_2<0$，火箭静不稳定
• 若气动压心在质心之后，即$b_2>0$，火箭静稳定

火箭稳定性分析

基本流程：

• 系数冻结时刻状态方程（起飞、气动力矩系数最大时、关机前）
• 简化的特征方程（是否有右半平面的根）
• 无控（开环稳定性）
• 模态的运动形式（根据特征根是实根还是复根判断）

起飞时刻稳定性

综上，在起飞时刻无控时，无论静稳定 $\left(b_2>0\right)$ 或静不稳定 $\left(b_2<0\right)$ ，姿态运动均不稳定

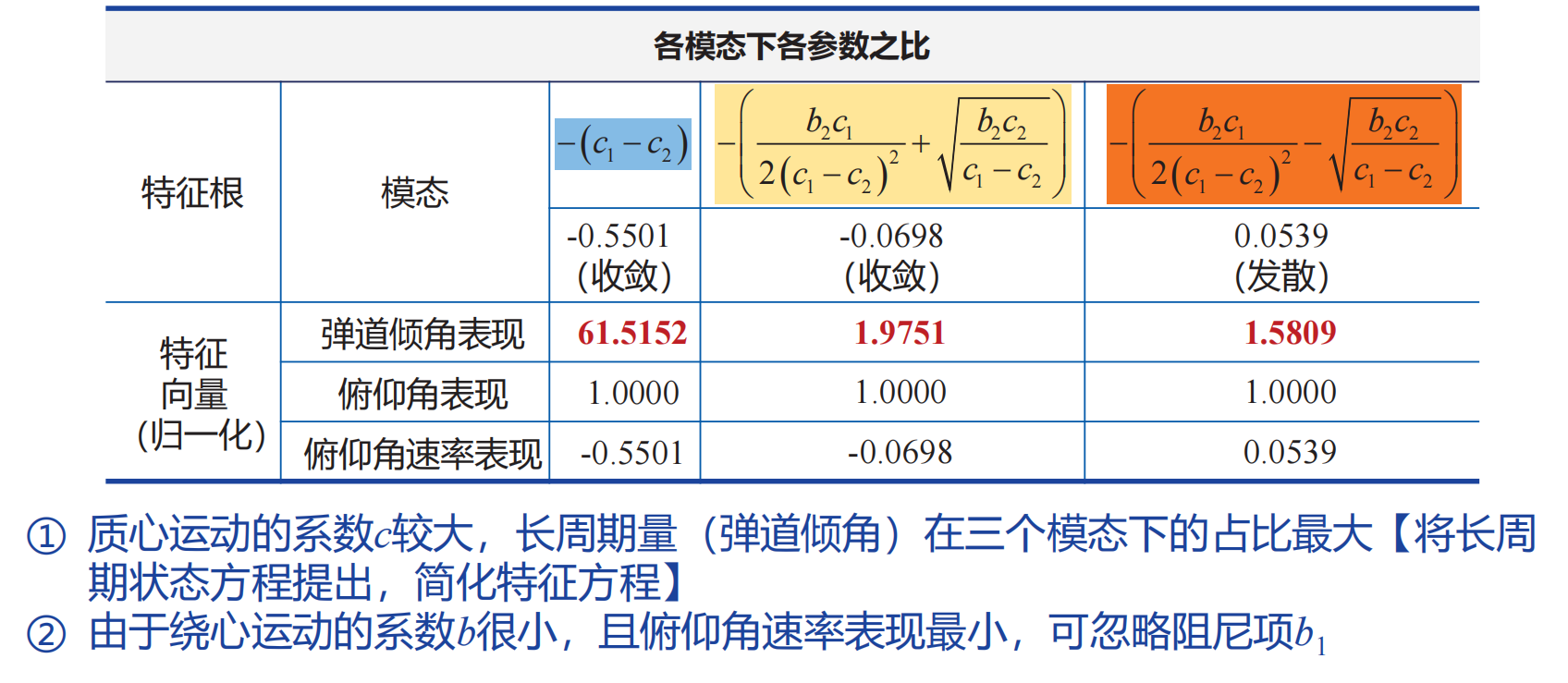
气动力矩系数最大时

在最大动压段无控时必然不稳定，同时：

• $b_2>0$静稳定，则重力作用下振荡缓慢发散
• $b_2<0$静不稳定，则在气动力矩作用下单调迅速发散

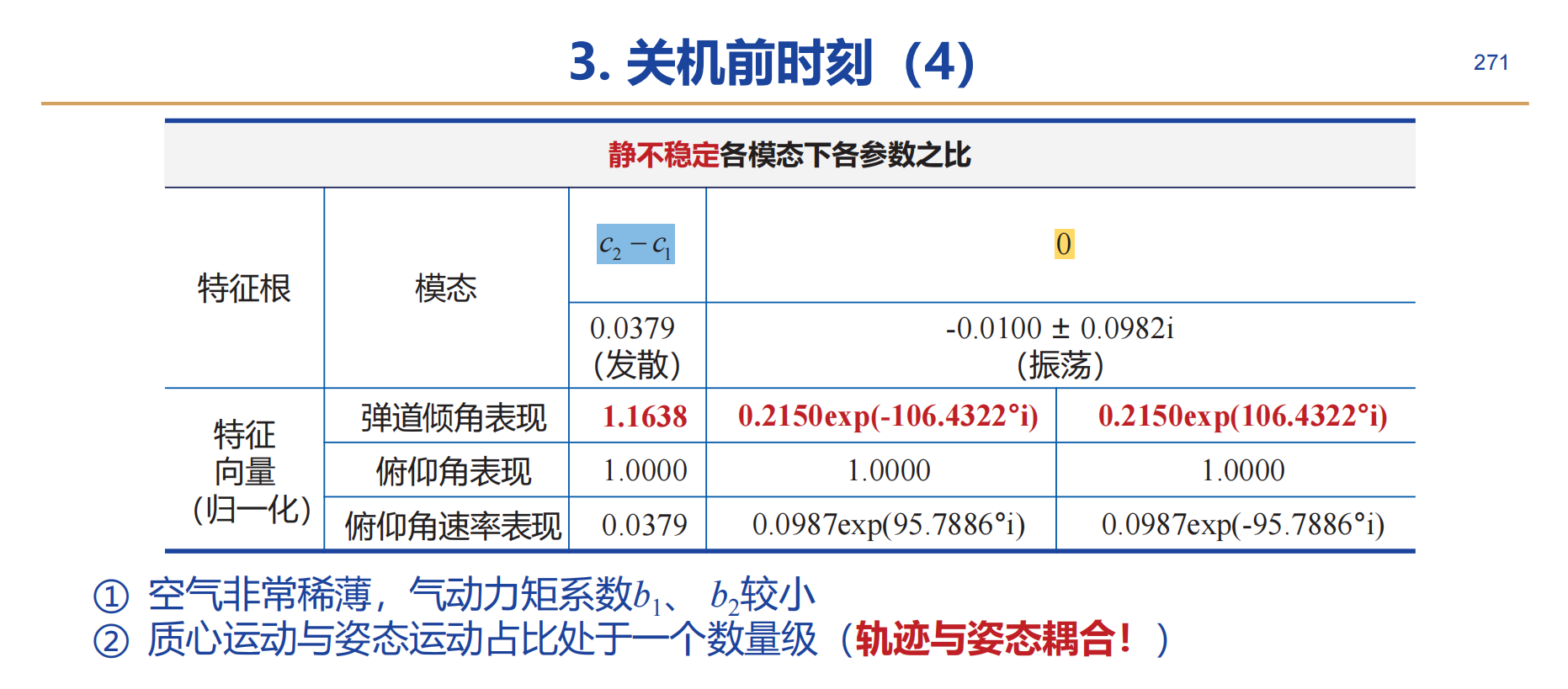
关机前时刻

系统在原点有两个特征根，一旦有外干扰就会发散

总结