坐标系之间的转换
四个主要坐标系之间的转换
四个坐标系和三组角度
- 发射点坐标系
- 本体系
- 速度坐标系
- 弹道坐标系
- 姿态角——俯仰角、偏航角、滚转角
- 气流角——攻角、侧滑角
- 弹道角——弹道倾角/速度倾角、弹道偏角/航向角
转换关系
到
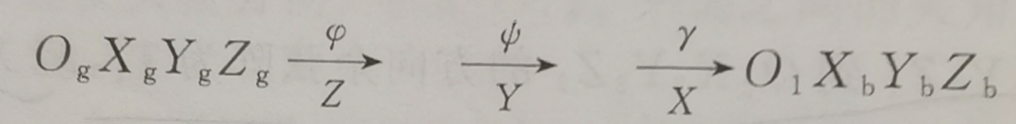
到

到
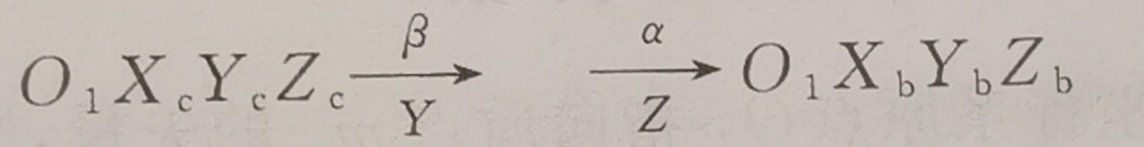
到
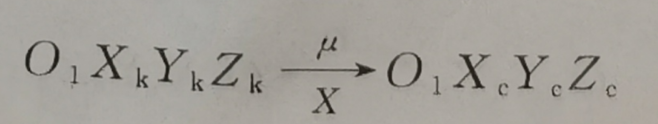
这里出现了一个没有见过的角度,我们回顾坐标系定义可知,和的x轴都是速度矢量方向,不同的是y轴
- 关注于飞行器弹道,所以y轴与“飞行器当前位置的铅垂面”内
- 关注于飞行器姿态,所以y轴在“飞行器当前纵平面”内
这么一看,他们的变换关系确实应该就是绕x轴旋转了一个角度,把原本在“铅垂面”内的y轴转到了“纵平面”内
的物理含义:飞行器的主升力方向(纵平面内)与当地铅垂面之间的夹角
对于面对称的升力体飞行器(如飞机),横侧向速度方向的改变主要依靠主升力面产生的升力(依靠滚转改变主升力方向,产生横侧向升力),此时表示的就是升力用于横侧向机动的分量大小
对于轴对称的旋成式飞行器(如火箭、弹头),由于过弹体纵轴的各个截面面积相同,在横侧向机动时无需调整滚动姿态将升力进行横侧向投影,这种情况下一般保持弹体滚动稳定,不考虑倾侧角,即
转换关系总结
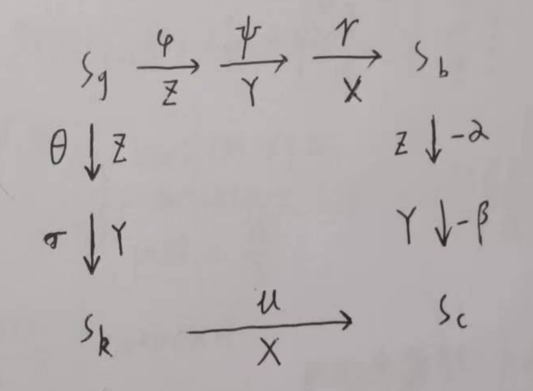
注意
书上的攻角侧滑角是从系转换到系时为正,如果反过来转换的话,相应的角度也应该变成负的
这个可以结合角度的定义来理解,当时我们发现只有攻角和侧滑角是向下、向右为正,俯仰角和偏航角、弹道倾角和弹道偏角,都是向上、向左为正,结合下面这个图
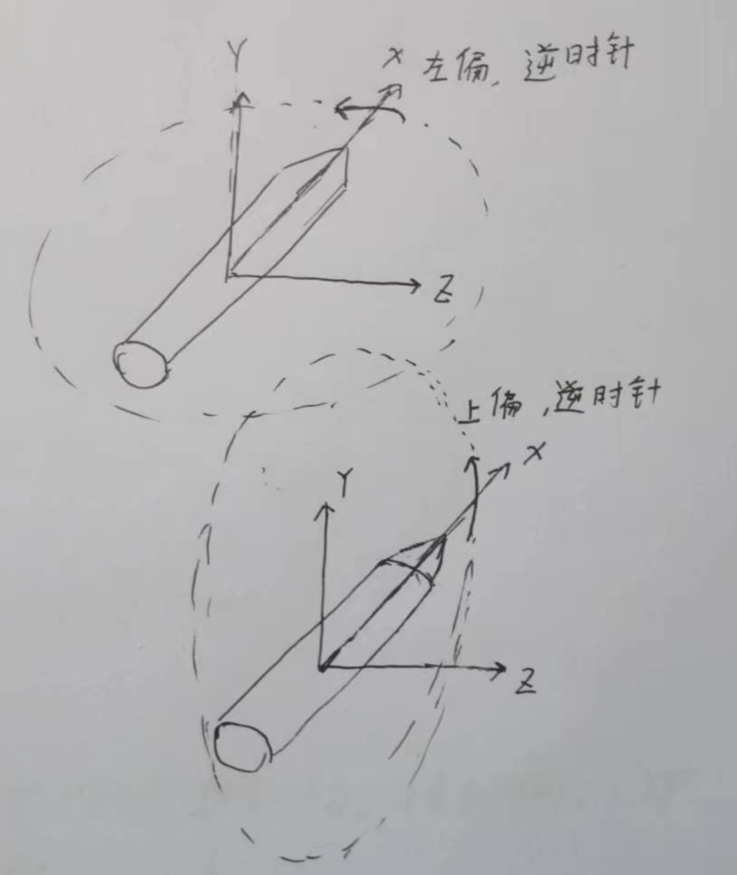
我们可以发现,在本体系中看的话,向上、向左分别代表着Y轴逆时针转、和Z轴逆时针转,逆时针方向为正,所以此时旋转角度是正的。
只有从到的时候是负的