飞行器姿态的表示

讨论3组重要的角度

四个主要坐标系

具体定义参见常用坐标系

• 发射点坐标系$S_g$
• 本体系$S_b$
• 速度坐标系$S_c$
• 弹道坐标系$S_k$

三组规定好的角

• 姿态角——俯仰角$\phi$、偏航角$\psi$、滚转角$\gamma$
• 气流角——攻角$\alpha$、侧滑角$\beta$
• 弹道角——弹道倾角/速度倾角$\theta$、弹道偏角/航向角$\sigma$

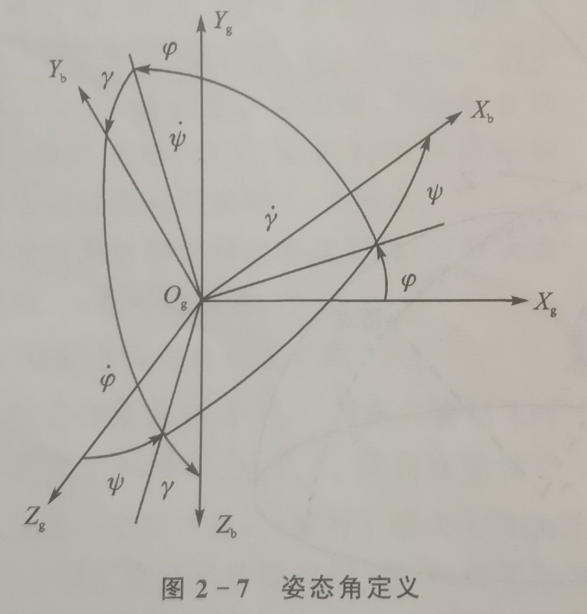
姿态角定义

名称	定义	备注
俯仰角$\phi$	$O_1X_b$轴在$X_gO_gY_g$平面的投影，与$O_gX_g$之间的夹角，抬头为正	$O_1X_b$轴指向飞行器前方 $X_gO_gY_g$平面是发射时飞行器“垂直方向”的平面（因为$S_g$系Y轴“向上”） $O_gX_g$轴指向发射方向在发射点水平面的投影 相当于“飞行器前方”相对于“发射时的前方”抬头的角度
偏航角$\psi$	$O_1X_b$轴与$X_gO_gY_g$平面的夹角，向左为正	$O_1X_b$轴指向飞行器前方 $X_gO_gY_g$平面是发射时飞行器“垂直方向”的平面（因为$S_g$系Y轴“向上”） 相当于“飞行器前方”相对于“发射时的竖直面”左转的角度
滚转角$\gamma$	$O_1Z_b$轴与$O_1X_b$和$O_1Z_g$两轴构成平面之间的夹角，右滚动为正	$O_1X_b$轴指向飞行器前方 $O_1Z_g$轴指向“发射时”飞行器右方 上述两轴组成“没有滚转，只改变俯仰”的平面 $O_1Z_b$轴指向飞行器右方 相当于“飞行器当前右机翼”与上述平面的夹角，即为滚转的角度

姿态角图示

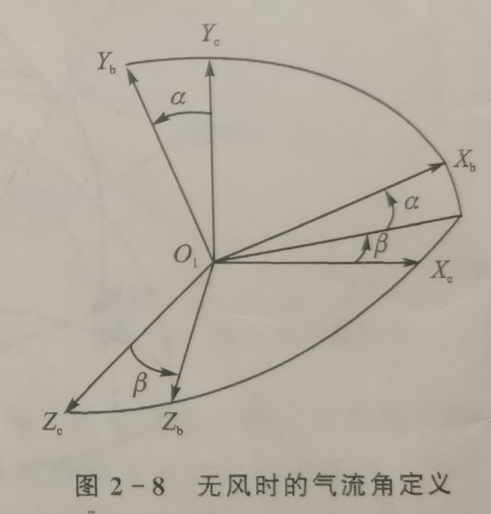
无风时气流角定义

名称	定义	备注
攻角$\alpha$	$O_1X_c$轴在$X_bO_1Y_b$平面的投影，与$O_1X_b$之间的夹角，向下为正	$O_1X_c$轴指向速度方向 $X_bO_1Y_b$是飞行器的“纵向”平面 $O_1X_b$轴指向飞行器前方 相当于“飞行器速度前方”相对于“飞行器物理上的前方”下压的角度
侧滑角$\beta$	$O_1X_c$轴与$X_bO_1Y_b$平面的夹角，向右为正	$O_1X_b$轴指向飞行器前方 $X_gO_gY_g$平面是“垂直方向”的平面（因为$S_g$系Y轴“向上”） 相当于“飞行器速度前方”相对于“飞行器当前竖直面”右转的角度

提示

可以发现攻角和俯仰角、侧滑角和偏航角有相当多的相似之处

有点“攻角是速度的俯仰角，侧滑角是速度的偏航角”的意思，但是注意有三点不同：

• 攻角（侧滑角）是相对于当前飞行器姿态，而俯仰角（偏航角）是相对于发射时的方向
• 俯仰角的定义是向上为正，而攻角是向下为正
• 偏航角的定义是向左为正，而侧滑角是向右为正

无风时气流角图示

注意

这是无风是气流角的定义，如果是有风情况，攻角和侧滑角都需要加上一个附加项

• 附加攻角$\alpha_w$
• 附加侧滑角$\beta_w$

他们分别定义为飞行器速度为0时，气流相对于本体系的攻角与侧滑角

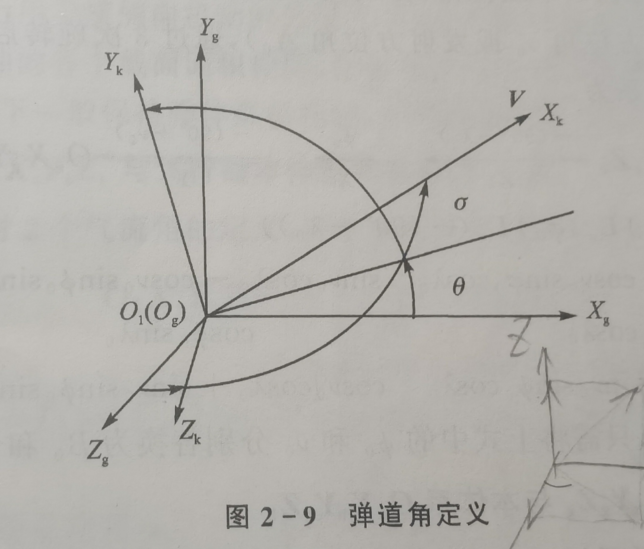
弹道角定义

名称	定义	备注
速度倾角$\theta$	速度矢量在$X_gO_gY_g$平面内的投影与$O_gX_g$轴的夹角，向上为正
航向角$\sigma$	速度矢量在$X_gO_gY_g$平面之间的夹角，向左为正

提示

速度倾角和俯仰角、航向角和偏航角也有异曲同工之妙

类似“速度倾角是速度相对发射点坐标系的俯仰角，侧滑角是速度相对发射点坐标系的偏航角”，注意：

• 速度倾角（航向角）是速度前方相对发射点坐标系，俯仰角（偏航角）是飞行器前方相对于发射点坐标系

弹道角图示

总结

3组角度，其实就是“飞行器前方、速度前方”相对“本体坐标系、发射点坐标系”的角度

• 飞行器前方——本体坐标系（飞行器前方就是$O_1X_b$轴，所以没有角度）
• 飞行器前方——发射点坐标系（俯仰角$\phi$、偏航角$\psi$、滚转角$\gamma$）
• 速度前方——本体坐标系（攻角$\alpha$、侧滑角$\beta$）
• 速度前方——发射点坐标系（弹道倾角/速度倾角$\theta$、弹道偏角/航向角$\sigma$）

怎样记忆字母？

• 俯仰——fu yang——首字母F——$\phi$读作/faɪ/
• 偏航——pian hang——首字母P——$\psi$读作/psaɪ/
• 滚转是剩下的那一个
• 攻角和侧滑角直接记住
• $\sigma$不对称所以是弹道偏角，另一个对称的$\theta$就是弹道倾角