哥氏加速度

研究运载体在地球表面附近航行的绝对加速度

结论

$$\left.\frac{d^2 \boldsymbol{R}}{d t^2}\right|_i=\left.\frac{d^2 \boldsymbol{R}_0}{d t^2}\right|_i+\left.\frac{d^2 \boldsymbol{r}}{d t^2}\right|_e+2 \omega_{i e} \times\left.\frac{d \boldsymbol{r}}{d t}\right|_e+\boldsymbol{\omega}_{i e} \times\left(\boldsymbol{\omega}_{i e} \times \boldsymbol{r}\right)$$

从运动学知，当动点相对某一动参考系作相对运动，同时这个动参考系又在做牵连转动时，则该动点将具有哥氏加速度$a_c$：

$$\boldsymbol{a}_c=2 \boldsymbol{\omega} \times \boldsymbol{v}_r$$

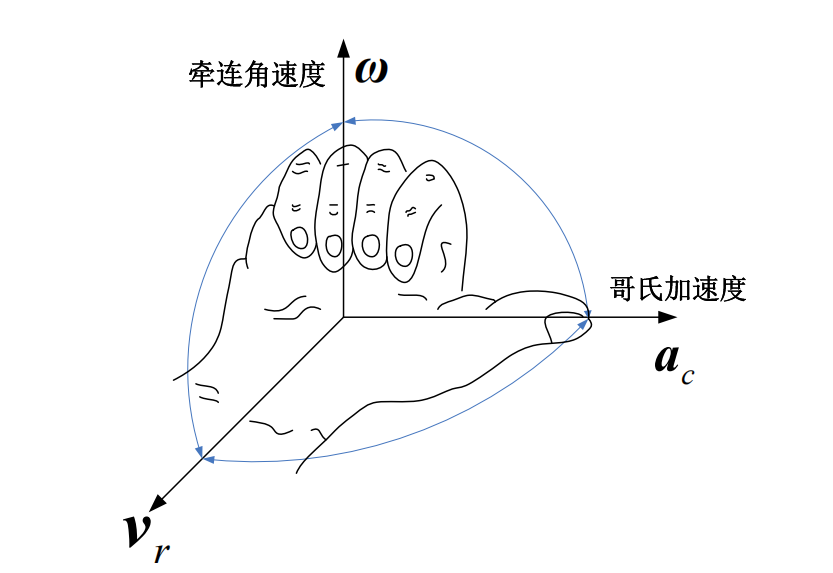
这个加速度的实际是惯性的表现，可以理解为两方面

当小球沿杆向远离圆心的方向移动时：

• 半径增大，切向速度大小需要增大
• 圆盘旋转，法向速度方向需要改变

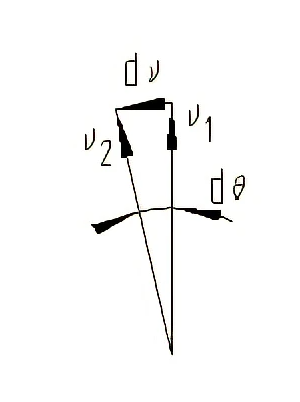
当动点的牵连运动为转动时，牵连运动会使相对速度的方向不断发生改变，而相对运动又使牵连速度的大小不断发生改变。这两种原因都造成了同一方向上附加的速度变化率，该附加的速度变化率即为哥氏加速度。简而言之，哥氏加速度是由于相对运动与牵连运动的相互影响而形成的。

参考来源：知乎——怎样简易的理解科氏加速度？

绝对加速度

当动点的牵连运动为转动时，动点的绝对加速度应等于相对加速度、牵连加速度与哥氏加速度的矢量和：

$$\boldsymbol{a}=\boldsymbol{a}_r+\boldsymbol{a}_e+\boldsymbol{a}_c$$

下面讨论运载体在地球表面附近航行时所受的加速度

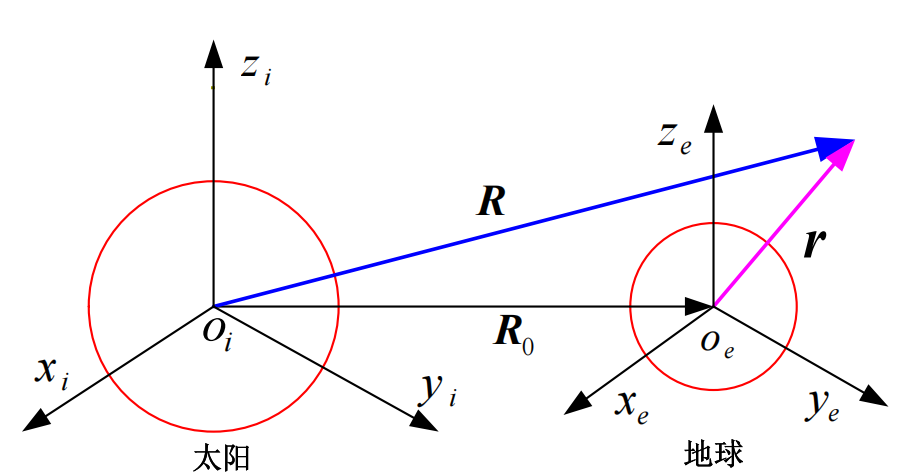
这里选取太阳为惯性系（虽然实际上也不是），地球的坐标系在惯性空间内有平移和旋转，飞行器在地球坐标系下的矢径是r

对$R=R_0+r$求两次导之后的结果为：

$$\left.\frac{d^2 \boldsymbol{R}}{d t^2}\right|_i=\left.\frac{d^2 \boldsymbol{R}_0}{d t^2}\right|_i+\left.\frac{d^2 \boldsymbol{r}}{d t^2}\right|_e+2 \boldsymbol{\omega}_{i e} \times\left.\frac{d \boldsymbol{r}}{d t}\right|_e+\boldsymbol{\omega}_{i e} \times\left(\boldsymbol{\omega}_{i e} \times \boldsymbol{r}\right)$$

第一次求导：

$$\left.\frac{d \boldsymbol{R}}{d t}\right|_i=\left.\frac{d \boldsymbol{R}_0}{d t}\right|_i+\left.\frac{d \boldsymbol{r}}{d t}\right|_i$$

其中

$$\left.\frac{d \boldsymbol{r}}{d t}\right|_i=\left.\frac{d \boldsymbol{r}}{d t}\right|_e+\boldsymbol{\omega}_{i e} \times \boldsymbol{r}$$

它表示了向量的绝对变率和相对变率的关系，称为哥氏方程，也叫哥氏转动坐标定理

在固定坐标系中，一个向量对时间的变化率（绝对变化率）等于同一向量在动坐标系中对时间的变化率（相对变化率）与动坐标系对固定坐标系的旋转角速度向量和该向量本身的向量积之和。

【后面一项看起来有点像$v=\omega*r$】

最后的方程为

$$\left.\frac{d \boldsymbol{R}}{d t}\right|_i=\left.\frac{d \boldsymbol{R}_0}{d t}\right|_i+\left.\frac{d \boldsymbol{r}}{d t}\right|_e+\boldsymbol{\omega}_{i e} \times \boldsymbol{r}$$

第二次求导：

$$\frac{d}{d t}\left(\left.\frac{d \boldsymbol{R}}{d t}\right|_i\right)_i=\left.\frac{d^2 \boldsymbol{R}}{d t^2}\right|_i$$

$$\frac{d}{d t}\left(\left.\frac{d \boldsymbol{R}_0}{d t}\right|_i\right)_i=\left.\frac{d^2 \boldsymbol{R}_0}{d t^2}\right|_i$$

$$\frac{d}{d t}\left.\left(\left.\frac{d \boldsymbol{r}}{d t}\right|_e\right) \right|_i=\frac{d}{d t}\left.\left.\left(\left.\frac{d \boldsymbol{r}}{d t}\right|_e \right)\right|_e+\omega_{i e} \times\left.\frac{d \boldsymbol{r}}{d t}\right|_e=\left.\frac{d^2 \boldsymbol{r}}{d t^2}\right|_e+\omega_{i e} \times\left.\frac{d \boldsymbol{r}}{d t}\right|_e\right.$$

$$\left.\frac{d\left(\boldsymbol{\omega}_{i e} \times \boldsymbol{r}\right)}{d t}\right|_i=\boldsymbol{\omega}_{i e} \times\left.\frac{d \boldsymbol{r}}{d t}\right|_i+\left.\frac{d \boldsymbol{\omega}_{i e}}{d t}\right|_i \times \boldsymbol{r}$$

其中比较难搞的是第三行的式子，但是可以把

$$\frac{d \boldsymbol{r}}{d t}$$

整体理解为一个在旋转坐标系中的矢量（实际也就是速度在地球坐标系中），然后再用哥氏方程。

最终得到的绝对加速度方程为：

$$\left.\frac{d^2 \boldsymbol{R}}{d t^2}\right|_i=\left.\frac{d^2 \boldsymbol{R}_0}{d t^2}\right|_i+\left.\frac{d^2 \boldsymbol{r}}{d t^2}\right|_e+2 \omega_{i e} \times\left.\frac{d \boldsymbol{r}}{d t}\right|_e+\boldsymbol{\omega}_{i e} \times\left(\boldsymbol{\omega}_{i e} \times \boldsymbol{r}\right)$$

其中：