捷联式惯导系统
捷联式惯导系统简介、工作过程、即时修正算法
定义
平台式惯导的缺点:
- 平台式惯导系统结构复杂,故障率较高
捷联式惯导的简述:
- 将惯性器件(陀螺仪和加速度计)直接安装在载体上的一种惯导系统
从结构上说,二者的主要区别:
- 去掉了实体的惯性平台而代之以存贮在计算机里的“数学平台”
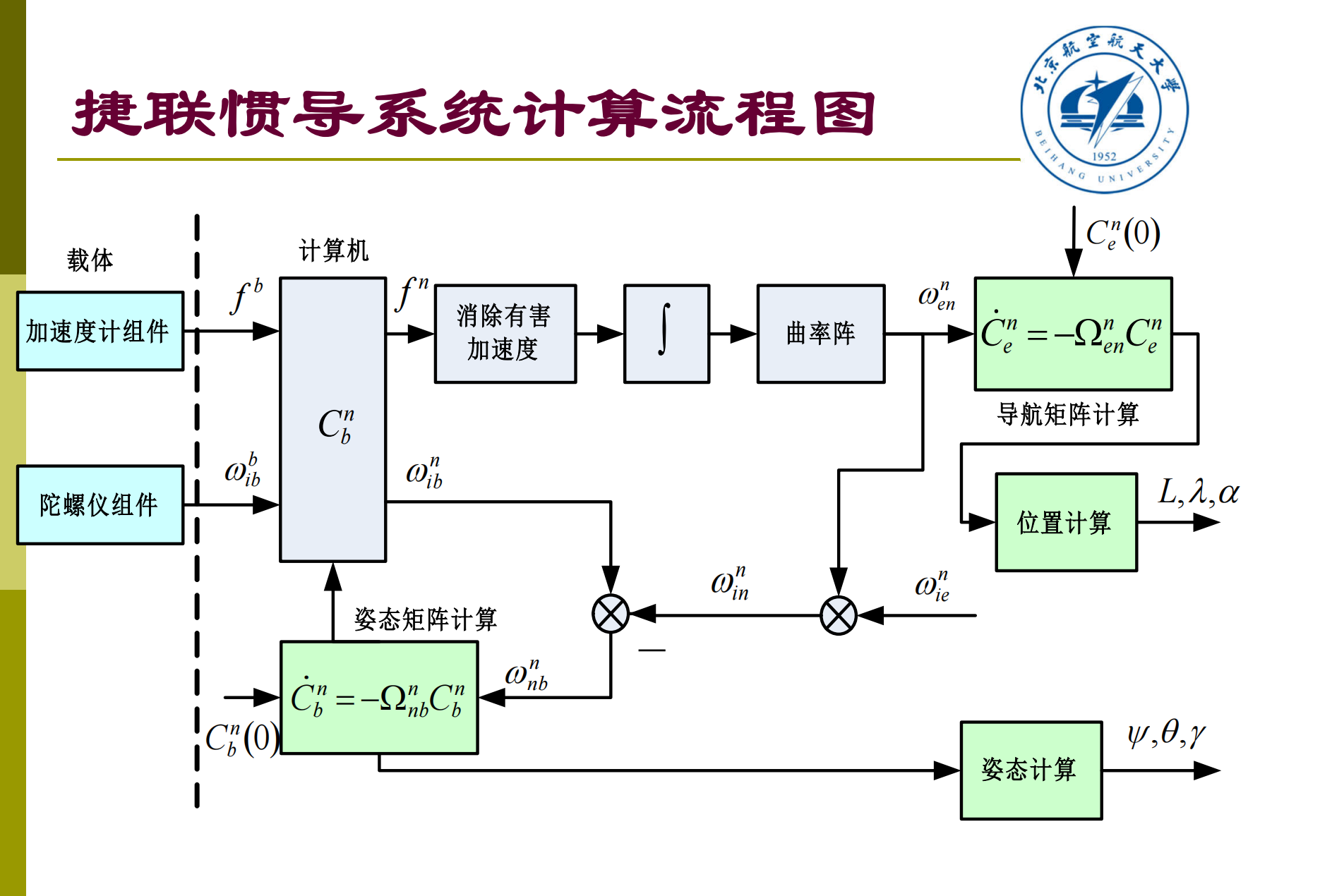
计算机必须能实时地提供方向余弦矩阵 ,才 能实时地把 转换为 。
技术难点
对惯性器件技术的要求更加严格和苛刻
由于实体平台对惯性器件所起的运动隔离作用已不复存在,惯性器件将不得不在相当恶劣的环 境下工作。要求陀螺仪能测量小至 0.01°/ h ,大至 400°/ s 的转动角速度,其动态量程达 10^8^
载体的运动冲击和振动也将严重影响惯性器件的性能
对计算机的计算速度和精度也提出更高的要求
由于借助计算机实现了“数学平台”,因而所要求的软件比平台式系统要多得多。
特别是要实现实时运算,对运算精度和速度都有很高的要求。
特点概括
- 取消了实体平台,代之以大量的实时软件,结果大大降低了系统体积、重量和成本
- 减少了系统中的机电元件,对加速度计和陀螺仪容易实现多余度配置方案,因此工作的可靠性大大提高
- 较平台系统维护简便,故障率低
- 由于动态环境恶劣,故对惯性器件的要求比平台系统高
加速度数学模型回顾
- 静态数学模型——线运动环境下,“加速度计输出”与“加速度输入”之间的关系
- 动态数学模型——角运动环境下,“加速度输出”与“加速度、角加速度输入”之间的关系
工作过程
- 系统的启动和自检
- 系统的初始化
- 惯性器件的误差补偿
- 姿态矩阵的计算
- 导航参数的计算
- 制导和控制信息的提取
即时修正算法
- 欧拉角法(三参数法)——可能存在奇点
- 四元数法(四参数法)——只需要进行加减法与乘法运算,求解的计算量要比欧拉角法少得多。
- 方向余弦法(九参数法)——方程数变多,但可以之间求出捷联矩阵T
由于位置矩阵的变化比姿态矩阵慢得多,不存在明显的非正交化误差,无需进行正交化处理
位置矩阵的即时修正往往采用方向余弦法