系统误差

误差来源、误差方程、影响误差的因素

误差源

这里以指北惯导系统为例

C_t^p=C_c^p C_t^c \quad \phi=\Psi+\theta

上式的意义：通过引入计算机坐标系c，把平台系相对地理系的误差角 $\phi$ 分成了两部分:

一部分是计算机系相对地理系的误差角 $\boldsymbol{\theta}$ ，它主要反映了导航参数误差 $\delta L$ 及 $\delta \lambda$ 。这种误差通过给平台的指令角速率转化为平台误差角的一部分
另一部分是平台系相对计算机系的误差 $\psi$ ，它主要反映了陀螺平台自身的漂移角速度 $\varepsilon$ 以及施矩轴线偏离了正确位置所造成的平台误差角。

误差方程的建立

\left.\begin{array}{l} \delta L=L_c-L \\ \delta \lambda=\lambda_c-\lambda \\ \delta v_x=v_x^c-v_x^t \\ \delta v_y=v_y^c-v_y^t \end{array}\right\}

惯导平台的两个水平控制回路既有交联影响，同时又构成了一个大的闭环系统。因而误差量之间的相互影响也具有相同的特点。下图是惯性平台误差传递方向的示意图。

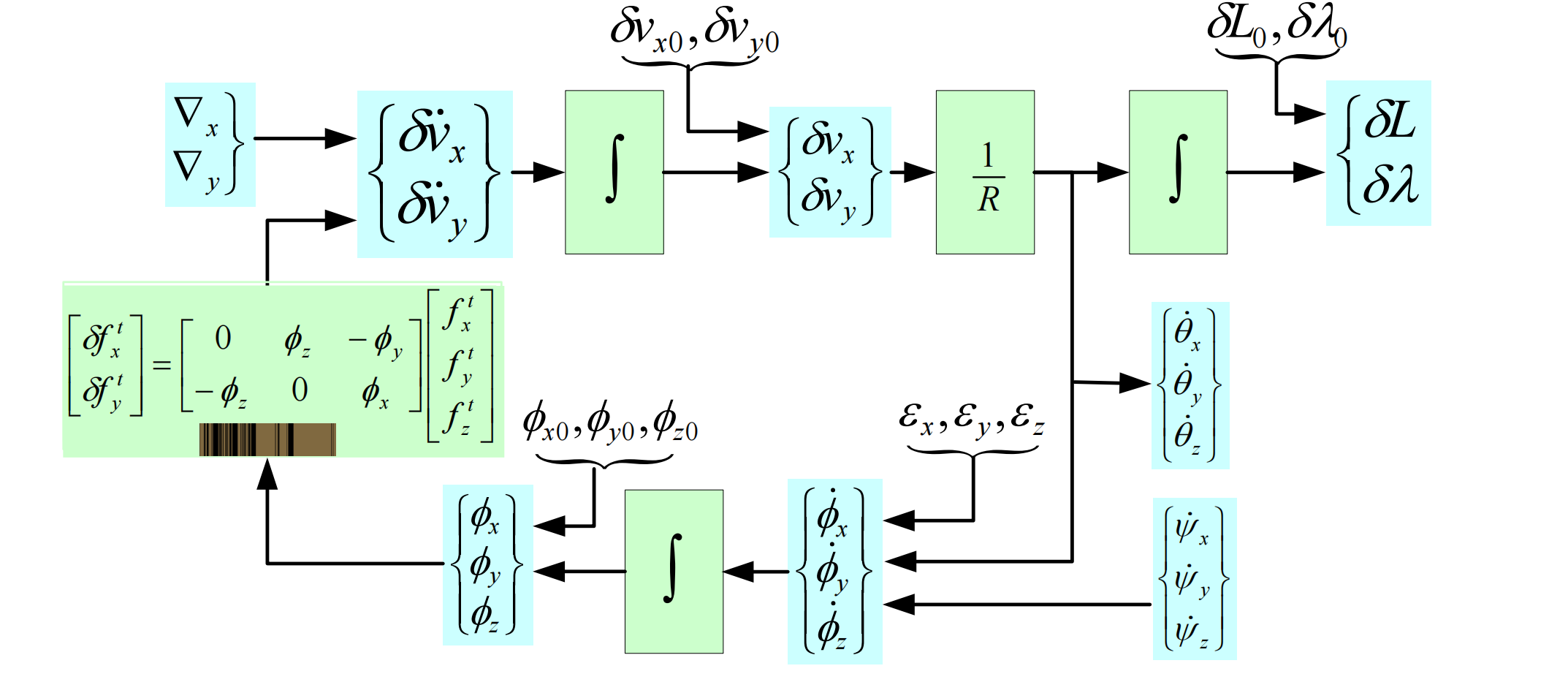
在建立系统误差方程时，也可以分为三段导出各误差量之间的函数关系，即速度误差方程、经纬度误差方程和平台误差方程。

找到或建立有关参数的原始方程
将原始方程进行微分处理，先把原始方程中对地理系的参数改写成对计算机系的参数，使之成为计算机解算方程，然后进行如下误差量代换，如令 $L_c=L+\delta L \quad \lambda_c=\lambda+\delta \lambda$ 等等，展开后再和原始方程相减，略去二阶小量，经过整理，即得到以误差量为基本参数的误差方程。
三段误差方程的总和就是系统误差方程。可利用拉氏变换将方程组表示成矩阵形式。

速度误差：

平台误差：