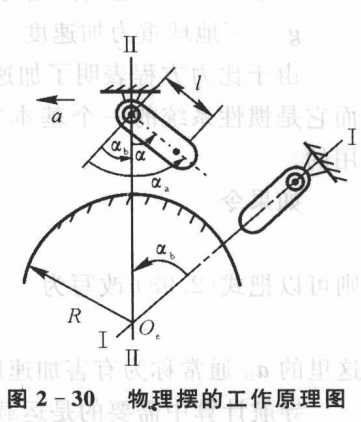
舒勒原理

舒勒摆与舒勒原理

问题引入

在惯性导航系统中，惯导平台要求精确地跟踪当地水平面（也就是惯导平台的垂直轴必须精确跟踪当地垂线），以便精确的给出加速度的基准。

怎么实现？

——利用单摆来指示垂线

普通摆如何指示垂线

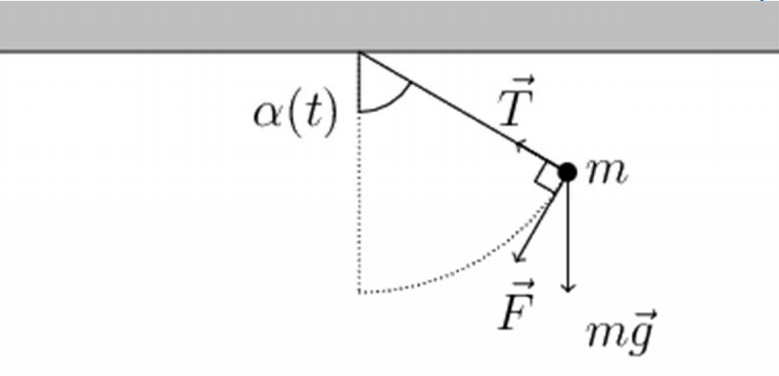
在载体上挂一个单摆时，如果载体静止或匀速直线运动，则单摆的平衡位置可以指示垂线方向

但是当载体作加速运动的时候，单摆的平衡位置不能指示地垂线，而是偏离了一个角度，此时单摆受到了加速度干扰

能否让单摆不受加速度干扰？

不受加速度干扰的单摆

参考：奇妙的舒勒周期84.4分钟 - 刘延柱的博文

• 一方面，有加速度时单摆会偏移一个角度
• 另一方面，地球是圆的，向前移动时地垂线也会偏移

可以猜想到，当摆长于地球半径相同时，不管支点如何移动，都不会影响摆锤及其平衡位置，即单摆始终指示地垂线而不受加速度的干扰【舒拉原理】

提示

铅锤方向的加速度不会干扰单摆的平衡位置，但水平方向的加速度会使单摆振动。若要单摆不受影响，必须使单摆的摆长具有地球半径的长度，这种单摆称为舒勒摆。可知这种单摆的固有震荡周期为84.4min

相关定义

舒勒原理

一个指示垂线的系统，如果其固有震荡周期为84.4min，则当运载体在地球表面易任意方式移动时，此装置将不受运载体加速度的干扰。

舒勒调谐

通过选择参数使得一个指示垂线的装置满足舒勒原理的条件，称为舒勒调谐

实际意义

只有使惯性导航系统成为舒勒调谐的系统，惯导系统才能不受运载体加速度的影响始终精确的跟踪当地水平面

证明过程

一、分析受力

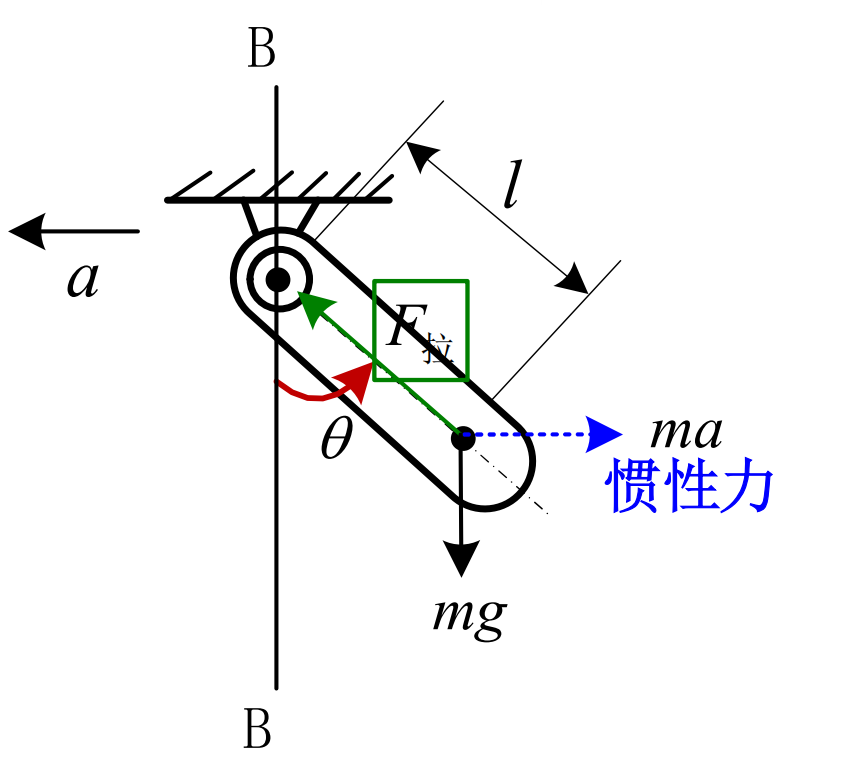
二、分析力矩

建立摆角微变方程

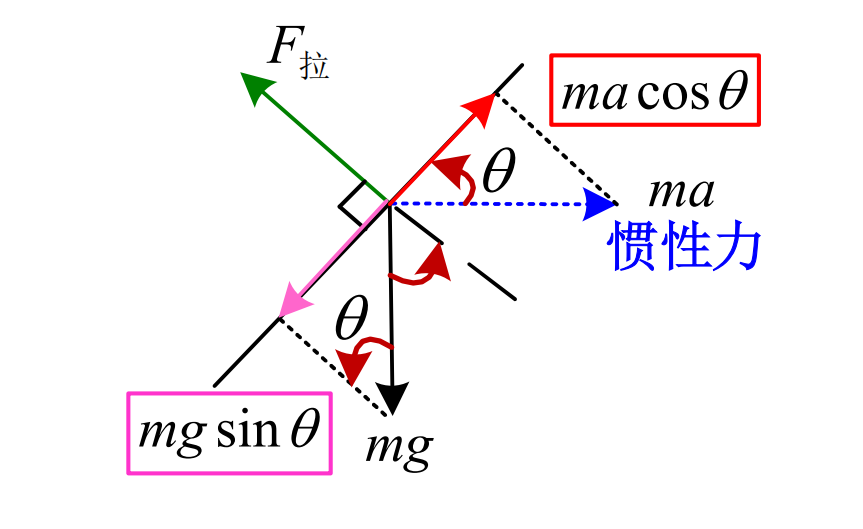
设单摆偏移竖直线的角度为$\theta$

• 重力产生的力矩：$mglsin\theta$
• 惯性力产生的力矩：$malcos\theta$

设单摆的转动惯量为$J$，则：

$$J \ddot{\theta}_\alpha=m l a \cos \theta-m g l \sin \theta$$

注意其中$\theta_\alpha$和$\theta$的区别，如下图，设支点从I运动一小段时间后来到了II的位置，则$\theta_\alpha$指的是相对于之前地垂线的偏角，而$\theta$是相对于现在地垂线的偏角，$\theta_b$是他们的差，他们之间满足关系

$$\left.\begin{array}{l} \alpha_{\mathrm{a}}=\alpha_{\mathrm{b}}+\alpha \\ \ddot{\alpha}_{\mathrm{a}}=\ddot{\alpha}_{\mathrm{b}}+\ddot{\alpha} \end{array}\right\}$$

已知：

$$J \ddot{\theta}_\alpha=m l a \cos \theta-m g l \sin \theta$$

其中

$$\ddot{\theta}_\alpha=\ddot{\theta}_b+\ddot{\theta}=\frac{a}{R}+\ddot{\theta}\\ cos\theta\approx1\ ,\ sin\theta\approx\theta$$

则：

$$\ddot{\theta}+\frac{m g l}{J} \theta=\left(\frac{m l}{J}-\frac{1}{R}\right) a$$