寻北仪
介绍寻北仪工作原理
简介
寻北仪是用来寻找某一位置的真北方位。
陀螺寻北仪又称陀螺罗盘。
工作原理
地球存在自转,自转角速度方向为地轴正北方向
将自转角速度投影到地理坐标系,则:
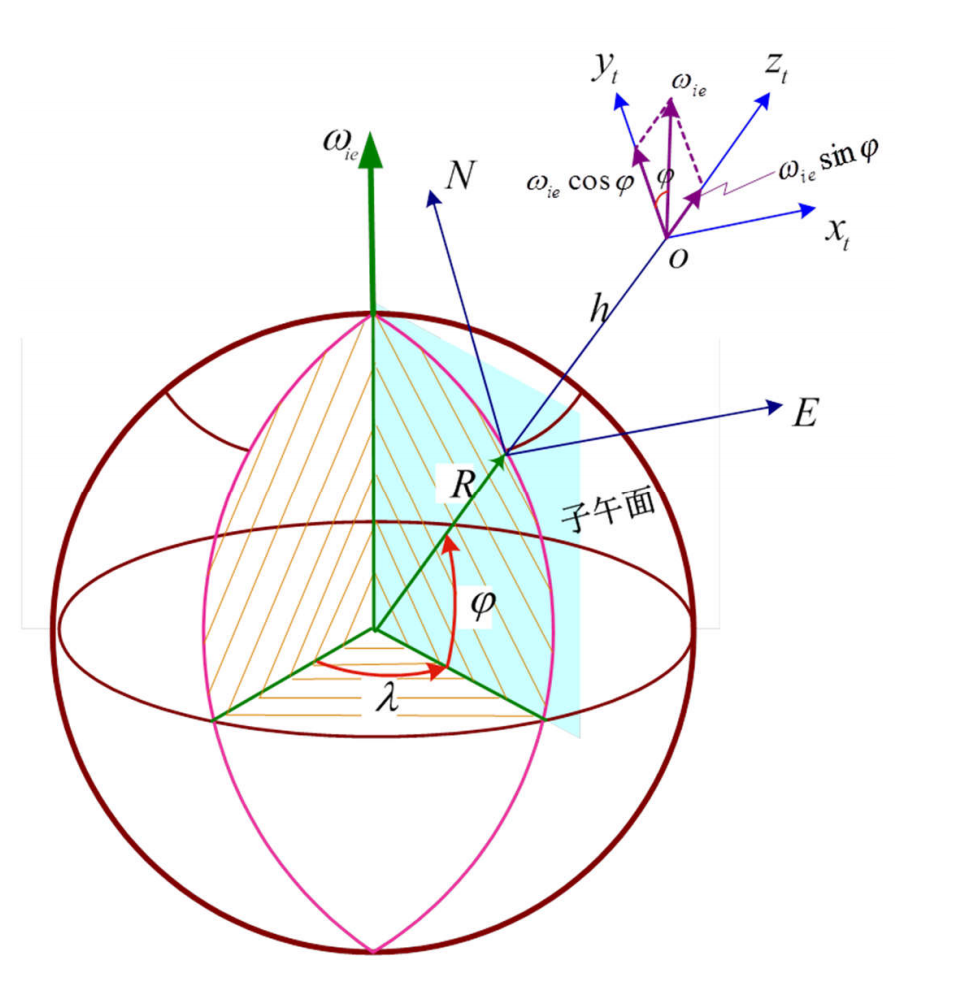
注意
地理坐标系的Y轴指向正北,所以在YOZ平面内,在X轴上没有分量
如果垂直于子午面来看
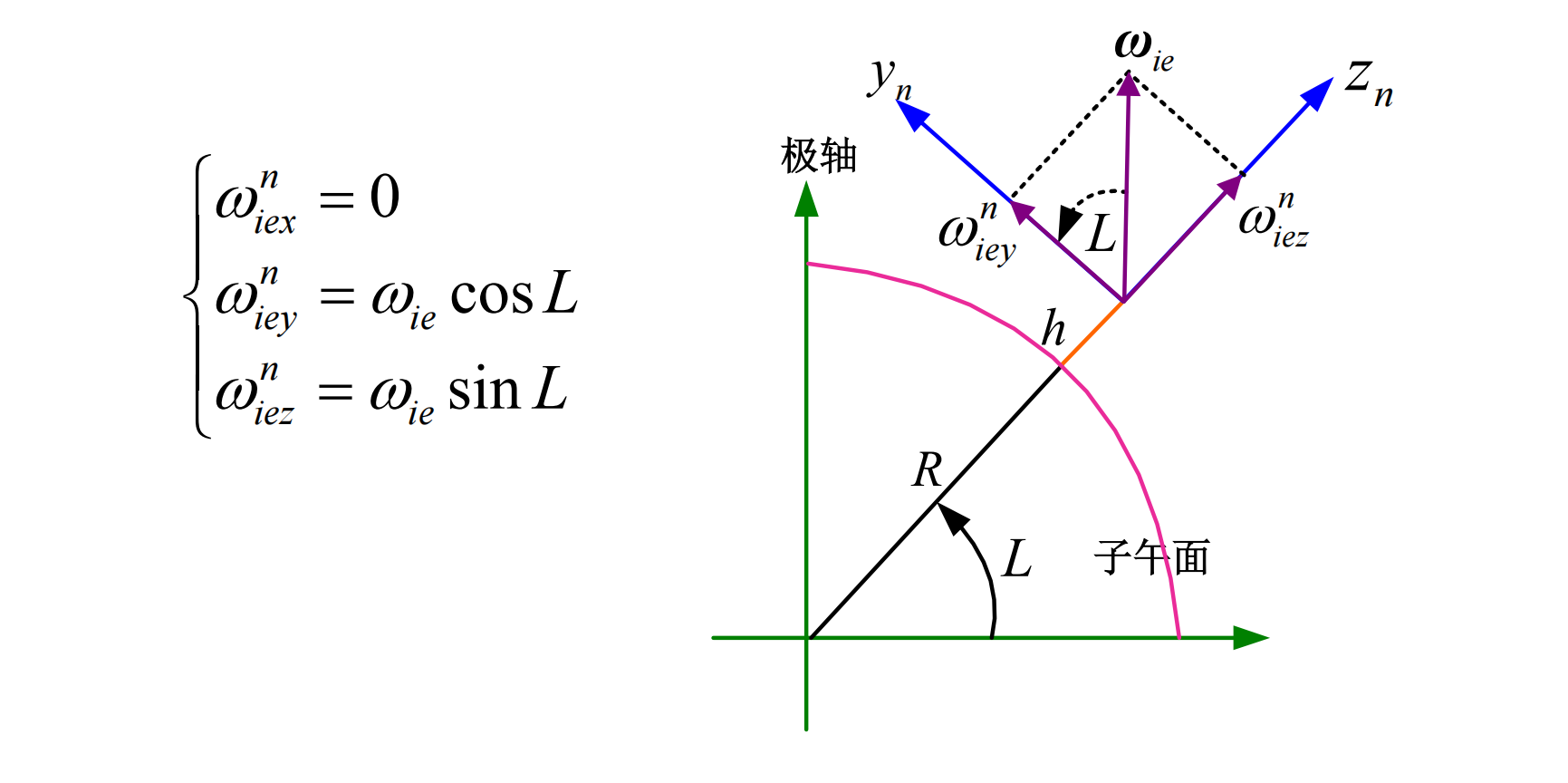
在水平面上看的话,因为角速度在x轴上没有分量,所以如果有陀螺仪来敏感加速度,那么当陀螺仪输出最大的时候,敏感轴的指向就是正北方向。
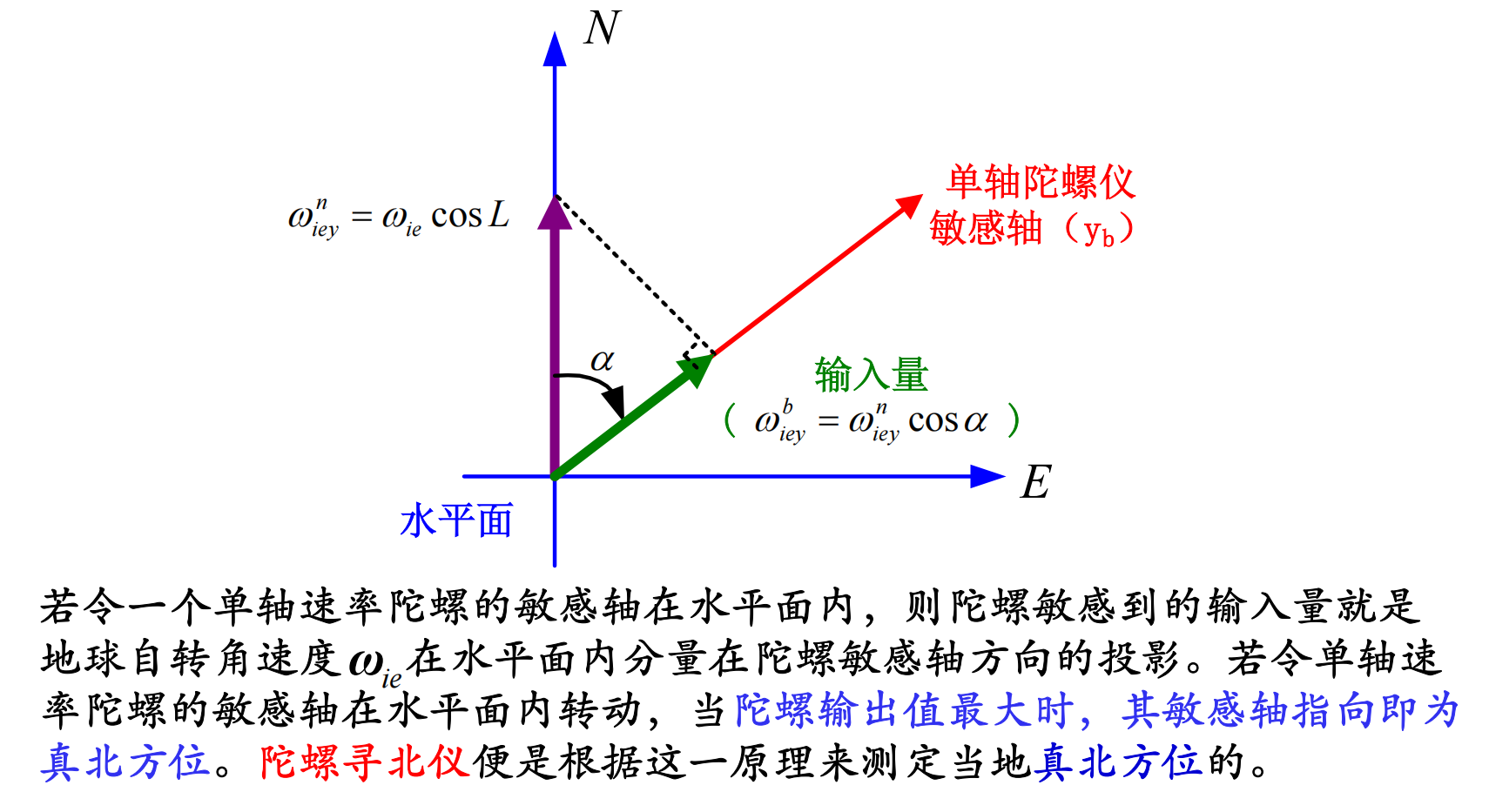
它的寻北过程无需外部参考,不受天气、昼夜时间、地磁场等条件的影响。
注意
实际寻北的过程也不需要去寻找输出最大的位置,可以通过依次转动固定角度,然后通过列方程计算的形式来得到陀螺敏感轴与真北方向的夹角。
用此方法测量,可以消除陀螺的零偏,也不需要知道测量地点的纬度值。如果测量地点的纬度 为已知值,那么可以只需测量1和3(或者2和4)两个位置便可以求出航向角,即