角位置与变换矩阵
方向余弦和欧拉角法
方向余弦法
这里有两个坐标系和,要表示他们之间的转换关系
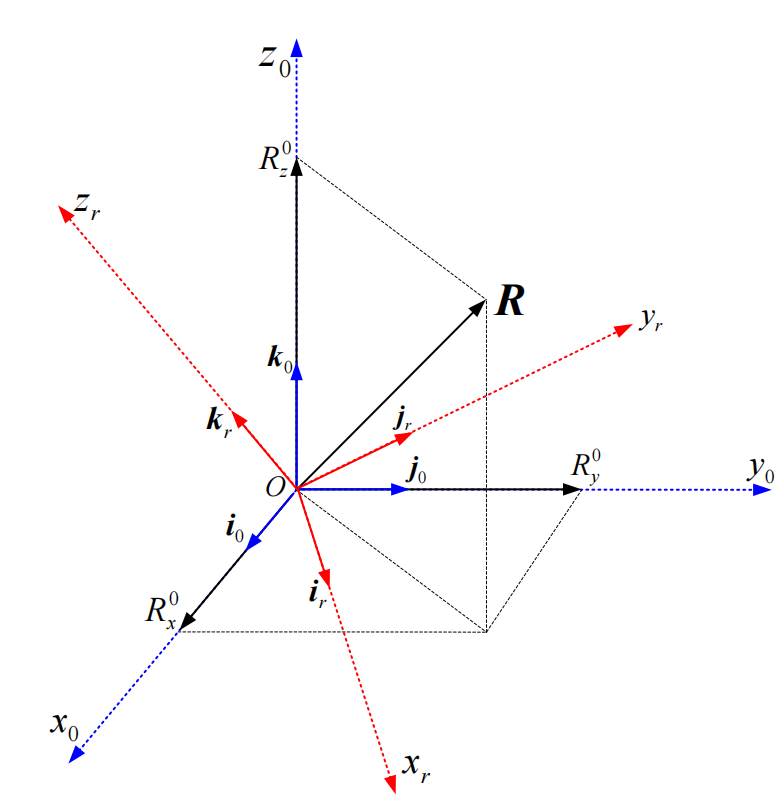
方向余弦法实际上就是把一个坐标系的三个单位矢量投影在另一个坐标系上。
提示
下图是r系到0系的变换矩阵,是将r系的、、在0系中的坐标表示出,每个都是一个3*1的列向量,再把他们排成3列,就是3*3的变换矩阵了
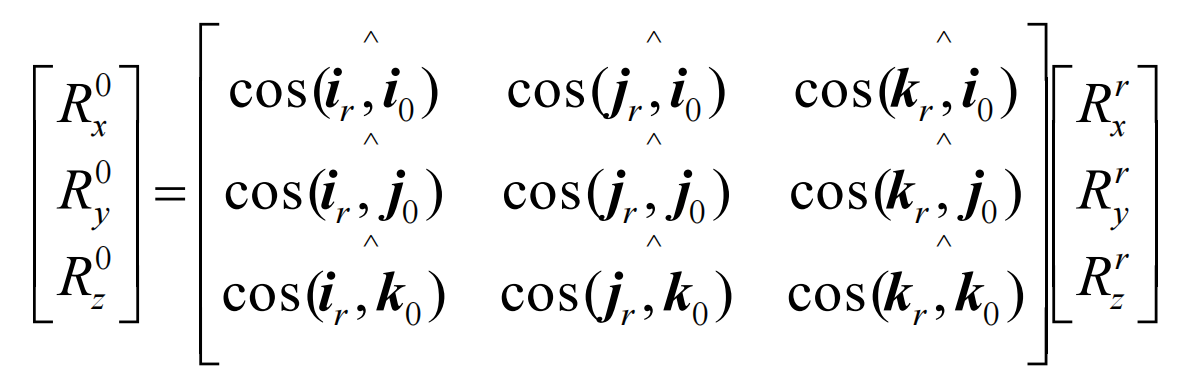
转换矩阵具有如下的性质
注意
除了方向余弦矩阵,欧拉角法写出的矩阵也有相同的性质,因为虽然计算方式不同,但是最后的转换矩阵在数学上相等。

欧拉角法
刚体坐标系相对参考坐标系的角位置,可以用三次独立的三个转角来确定,这就是欧拉法原理,这三个独立的角度称为欧拉角。
欧拉角的选取有3在*2*2共12种可能
对于定点转动的刚体,只要给定一组欧拉角,就能唯一确定刚体坐标系的九个方向余弦,从而唯一地确定刚体在空间的角位置。
所以实际上方向余弦法实际上也只有3个未知量,因为角度之间有一些约束